
分析 (1)由點K(-1,0)為直線l與拋物線C準線的交點可求拋物線C的方程,設直線l的方程為x=my-1與拋物線方程聯立,求出BD的方程,即可得出結論;
(2)設直線方程代入拋物線方程,根據$\overrightarrow{FA}$•$\overrightarrow{FB}$=$\frac{8}{9}$,結合韋達定理,即可求直線l的方程,再確定圓心與半徑,即可求△BDK內切圓M的方程.
解答 解:(1)證明:由題可知K(-1,0),拋物線的方程為y2=4x,則可設直線l的方程為x=my-1,
A(x1,y1),B(x2,y2),D(x1,-y1),
故$\left\{{\begin{array}{l}{x=my-1}\\{{y^2}=4x}\end{array}}\right.$整理得y2-4my+4=0,故$\left\{{\begin{array}{l}{{y_1}+{y_2}=4m}\\{{y_1}{y_2}=4}\end{array}}\right.$,
則直線BD的方程為$y-{y_2}=\frac{{{y_2}+{y_1}}}{{{x_2}-{x_1}}}({x-{x_1}})$,
即$y-{y_2}=\frac{4}{{{y_2}-{y_1}}}({x-\frac{y_2^2}{4}})$,
令y=0,得$x=\frac{{{y_1}{y_2}}}{4}=1$,
所以F(1,0)在直線BD上;
(2)由(1)可知$\left\{{\begin{array}{l}{{y_1}+{y_2}=4m}\\{{y_1}{y_2}=4}\end{array}}\right.$,
所以${x_1}+{x_2}=({m{y_1}-1})+({m{y_2}-1})=4{m^2}-2,{x_1}•{x_2}=\frac{y_1^2y_2^2}{16}=1$,
又$\overrightarrow{FA}$=(x1-1,y1),$\overrightarrow{FB}$=(x1-2,y2),
故$\overrightarrow{FA}$•$\overrightarrow{FB}$=x1x2-(x1+x2)+5=8-4m2,
則$8-4{m^2}=\frac{8}{9}$,
∴$m=±\frac{4}{3}$,
故直線l的方程為3x+4y+3=0或3x-4y+3=0,
又${y_2}-{y_1}=±\sqrt{{{({{y_2}+{y_1}})}^2}-4{y_1}{y_2}}=±\sqrt{16{m^2}-16}=±\frac{{4\sqrt{7}}}{3}$,
∴${k_{BD}}=\frac{{{y_2}+{y_1}}}{{{x_2}-{x_1}}}=\frac{4}{{{y_2}-{y_1}}}=±\frac{3}{{\sqrt{7}}}$,
故直線BD的方程$3x+\sqrt{7}y-3=0$或$3x-\sqrt{7}y-3=0$,
又KF為∠BKD的平分線,
故可設圓心M(t,0)(-1<t<1),M(t,0)到直線l及BD的距離分別為$\frac{{3|{t+1}|}}{5},\frac{{3|{t-1}|}}{4}$,
由$\frac{{3|{t+1}|}}{5}=\frac{{3|{t-1}|}}{4}$得$t=\frac{1}{9}$或t=9(舍去).
故圓M的半徑為$r=\frac{{3|{t+1}|}}{5}=\frac{2}{3}$,
所以圓M的方程為${({x-\frac{1}{9}})^2}+{y^2}=\frac{4}{9}$.
點評 本題考查拋物線的標準方程,考查直線與拋物線的位置關系,考查向量知識的運用,考查學生的計算能力,正確運用韋達定理是關鍵.


科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖所示,給出下列條件:
如圖所示,給出下列條件:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $({-∞,\frac{2}{5}}]$ | B. | $({-∞,\frac{1}{2}}]$ | C. | $({-∞,\frac{2}{3}}]$ | D. | (-∞,1] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
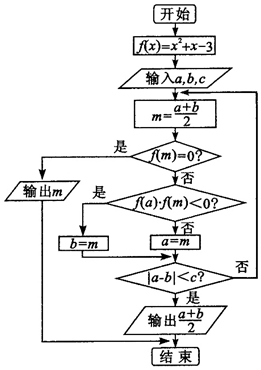
| A. | 1.125 | B. | 1.25 | C. | 1.3125 | D. | 1.375 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com