
| A. | ${a_n}=\frac{{n({n-1})}}{2}$ | B. | an=n(n-1) | C. | an=n-1 | D. | ${a_n}={2^n}-2$ |
分析 根據函數的零點的定義,構造兩函數圖象的交點,交點的橫坐標即為函數的零點,再通過數列及通項公式的概念得所求的解.
解答 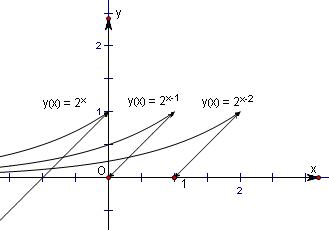 解:當x∈(-∞,0]時,
解:當x∈(-∞,0]時,
由g(x)=f(x)-x=2x-1-x=0,得2x=x+1.
令y=2x,y=x+1.
在同一個坐標系內作出兩函數在區間
(-∞,0]上的圖象,
由圖象易知交點為(0,1),
故得到函數的零點為x=0.
當x∈(0,1]時,x-1∈(-1,0],
f(x)=f(x-1)+1=2x-1-1+1=2x-1,
由g(x)=f(x)-x=2x-1-x=0,得2x-1=x.
令y=2x-1,y=x.
在同一個坐標系內作出兩函數在區間(0,1]上的圖象,由圖象易知交點為(1,1),
故得到函數的零點為x=1.
當x∈(1,2]時,x-1∈(0,1],f(x)=f(x-1)+1=2x-1-1+1=2x-2+1,
由g(x)=f(x)-x=2x-2+1-x=0,得2x-2=x-1.令y=2x-2,y=x-1.
在同一個坐標系內作出兩函數在區間(1,2]上的圖象,
由圖象易知交點為(2,1),故得到函數的零點為x=2.
依此類推,當x∈(2,3],x∈(3,4],…,x∈(n,n+1]時,
構造的兩函數圖象的交點依次為(3,1),(4,1),…,(n+1,1),
得對應的零點分別為x=3,x=4,…,x=n+1.
故所有的零點從小到大依次排列為0,1,2,…,n+1.其對應的數列的通項公式為an=n-1.
故選:C.
點評 本題主要考查了函數零點的概念及零點的求法、數列的概念及簡單表示;培養學生觀察、分析、歸納、推理的能力;解題中使用了數形結合及分類討論的數學方法和數學思想


科目:高中數學 來源: 題型:選擇題
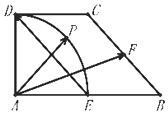 在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分別為
在直角梯形 ABCD 中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E,F 分別為| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{3\sqrt{2}}}{4}$ | C. | $\sqrt{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -7 | B. | -6 | C. | 7 | D. | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
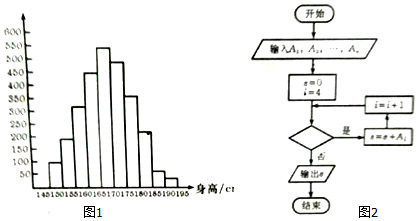
| A. | i<6 | B. | i<7 | C. | i<8 | D. | i<9 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [0,2] | B. | (0,2) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,-2] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{6}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
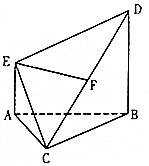 如圖,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F為CD中點.
如圖,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F為CD中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com