Question

若關于x的方程3x²-5x+a=0的一個根在（-2，0）內，另一個根在（1，3）內，求a的取值范圍．

Answer 1

解：設f（x）=3x²-5x+a，則f（x）為開口向上的拋物線（如圖所示）．

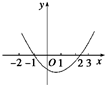
∵f（x）=0的兩根分別在區間（-2，0），（1，3）內，
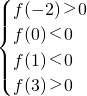
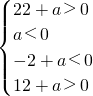
∴，即，解得-12＜a＜0．
∴所求a的取值范圍是（-12，0）．
分析：構造函數，利用關于x的方程3x²-5x+a=0的一個根在（-2，0）內，另一個根在（1，3）內，建立不等式，即可求a的取值范圍．
點評：本題考查方程根的分布，考查函數與方程思想，考查學生的計算能力，屬于中檔題．