
【題目】設函數![]() ;
;
(1)當![]() 時,解不等式
時,解不等式![]() ;
;
(2)若![]() ,且
,且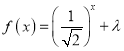 在閉區間
在閉區間![]() 上有實數解,求實數
上有實數解,求實數![]() 的范圍;
的范圍;
(3)如果函數![]() 的圖象過點
的圖象過點![]() ,且不等式
,且不等式![]() 對任意
對任意![]() 均成立,求實數
均成立,求實數![]() 的取值集合.
的取值集合.
【答案】(1)![]() (2)
(2)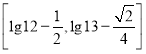 (3)
(3)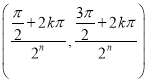 ,
,![]() ,
,![]()
【解析】
(1)根據對數的運算解不等式即可;
(2)根據![]() 可得
可得![]() 的解析式,由
的解析式,由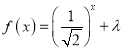 分離變量可得
分離變量可得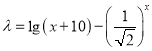 ,令
,令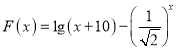 ,它在閉區間
,它在閉區間![]() 上的值域即為
上的值域即為![]() 的范圍;
的范圍;
(3)函數![]() 的圖象過點
的圖象過點![]() ,求
,求![]() 的解析式,可得
的解析式,可得![]() ,則不等式
,則不等式![]() 轉化為
轉化為![]() ,求解
,求解![]() ,又∵
,又∵![]() ,即
,即![]() ,
,![]() ,討論
,討論![]() 的范圍可得答案.
的范圍可得答案.
解:函數![]() ;
;
(1)當![]() 時,
時,![]() ,
,
那么:不等式![]() ;即
;即![]() ,
,
可得:![]() ,且
,且![]() ,
,
解得:![]() ,
,
∴不等式的解集為![]() ;
;
(2)∵![]() ,可得
,可得![]() ,
,
∴![]() ,
,
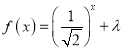 ,即
,即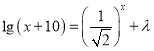 在閉區間
在閉區間![]() 上有實數解,
上有實數解,
可得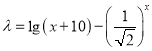 ,
,
令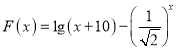 ,求在閉區間
,求在閉區間![]() 上的值域,
上的值域,
根據指數和對數的性質可知:![]() 是增函數,
是增函數,
∴![]() 在閉區間
在閉區間![]() 上的值域為
上的值域為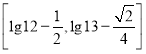 ,
,
故得實數![]() 的范圍是
的范圍是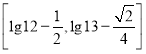 ;
;
(3)∵函數![]() 的圖象過點
的圖象過點![]() ,
,
則有:![]() ,
,
∴![]() ,
,
故![]() ,
,
那么:不等式![]() 轉化為
轉化為![]() ,
,
即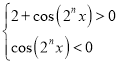 ,
,
∴![]() ,
,![]() ,
,
解得: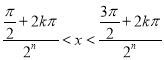 ,
,![]() ,
,
又∵![]() ,即
,即![]() ,
,
∴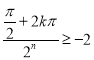 ,
,![]() ,
,
解得:![]() ,
,
∵![]() ,
,
∴![]() ,
,
故得任意![]() 均成立,實數
均成立,實數![]() 的取值集合為
的取值集合為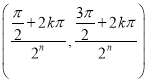 ,
,![]() ,
,![]() .
.


科目:高中數學 來源: 題型:
【題目】2019年9月24日國家統計局在慶祝中華人民共和國成立70周年活動新聞中心舉辦新聞發布會指出,1952年~2018年,我國GDP查679.1億元躍升至90.03萬億元,實際增長174倍;人均GDP從119元提高到6.46萬元,實際增長70倍.全國各族人民,砥礪奮進,頑強拼搏,實現了經濟社會的跨越式發展.如圖是全國2010年至2018年GDP總量![]() (萬億元)的折線圖.
(萬億元)的折線圖.

注:年份代碼1~9分別對應年份2010~2018.
(1)由折線圖看出,可用線性回歸模型擬合![]() 與年份代碼
與年份代碼![]() 的關系,請用相關系數加以說明;
的關系,請用相關系數加以說明;
(2)建立![]() 關于
關于![]() 的回歸方程(系數精確到0.01),預測2019年全國GDP的總量.
的回歸方程(系數精確到0.01),預測2019年全國GDP的總量.
附注:參考數據:![]() ,
,![]() ,
,![]() ,
,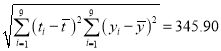 .
.
參考公式:相關系數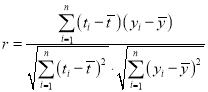 ;
;
回歸方程![]() 中斜率和截距的最小二乘法估計公式分別為
中斜率和截距的最小二乘法估計公式分別為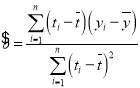 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正數數列![]() 、
、![]() 滿足:
滿足:![]() ≥
≥![]() ,且對一切k≥2,k
,且對一切k≥2,k![]() ,
,![]() 是
是![]() 與
與![]() 的等差中項,
的等差中項,![]() 是
是![]() 與
與![]() 的等比中項.
的等比中項.
(1)若![]() ,
,![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)求證:![]() 是等差數列的充要條件是
是等差數列的充要條件是![]() 為常數數列;
為常數數列;
(3)記![]() ,當n≥2(n
,當n≥2(n![]() )時,指出
)時,指出![]() 與
與![]() 的大小關系并說明理由.
的大小關系并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設m,n是兩條不同直線,α,β,γ是三個不同平面,給出下列四個命題:
①若m⊥α,n⊥α,則m∥n;②若α∥β,β∥γ,m⊥α,則m⊥γ;
③若m∥α,n∥α,則m∥n;④若m⊥α,m∥β,則α⊥β.
其中正確命題的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() (
(![]() )的一個焦點
)的一個焦點![]() 與拋物線
與拋物線![]() :
:![]() 的焦點重合,且離心率為
的焦點重合,且離心率為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過焦點![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點,與橢圓
兩點,與橢圓![]() 交于
交于![]() ,
,![]() 兩點,滿足
兩點,滿足![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的通項公式為
的通項公式為![]() (
(![]() ,
, ![]() ),數列
),數列![]() 定義如下:對于正整數
定義如下:對于正整數![]() ,
, ![]() 是使得不等式
是使得不等式![]() 成立的所有
成立的所有![]() 中的最小值.
中的最小值.
(1)若![]() ,
, ![]() ,求
,求![]() ;
;
(2)若![]() ,
, ![]() ,求數列
,求數列![]() 的前
的前![]() 項和公式;
項和公式;
(3)是否存在![]() 和
和![]() ,使得
,使得![]()
![]() ?如果存在,求
?如果存在,求![]() 和
和![]() 的取值范圍;如果不存在,請說明理由.
的取值范圍;如果不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com