
 已知直角梯形ABEF,∠A=∠B=90°,AB=1,BE=2,AF=3,C為BE的中點,AD=1,如圖(1),沿直線CD折成直二面角,連結部分線段后圍成一個空間幾何體(如圖2)
已知直角梯形ABEF,∠A=∠B=90°,AB=1,BE=2,AF=3,C為BE的中點,AD=1,如圖(1),沿直線CD折成直二面角,連結部分線段后圍成一個空間幾何體(如圖2)分析 (1)以點D為坐標原點,分別以DA,DC,DF所在直線為x軸,y軸,z軸建立空間直角坐標系.利用cos$<\overrightarrow{DB},\overrightarrow{EF}>$=$\frac{\overrightarrow{DB}•\overrightarrow{EF}}{|\overrightarrow{DB}||\overrightarrow{EF}|}$,即可得出.
(2)$G(\frac{1}{2},0,0)$,設平面$\overrightarrow{BEF}$的法向量為$\overrightarrow{{n}_{1}}$=(x,y,z),利用$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{BF}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{GF}=0}\end{array}\right.$,可得平面GBF的法向量$\overrightarrow{{n}_{1}}$=(4,-2,1),同理可得平面BEF的法向量$\overrightarrow{n_1}=(1,1,1)$.利用cos$<\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}>$=$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$,即可得出.
(3)連接AE,取中點為O,連接OA,OB,OC,OD,OE,由已知易得OA=OB=OC=OD=OE,可得DO長為所求球的半徑.
解答 解:(1)以點D為坐標原點,分別以DA,DC,DF所在直線為x軸,y軸,z軸建立空間直角坐標系.
D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),E(0,1,1),F(0,0,2).
$\overrightarrow{DB}$=(1,1,0),$\overrightarrow{EF}$=(0,-1,1),cos$<\overrightarrow{DB},\overrightarrow{EF}>$=$\frac{\overrightarrow{DB}•\overrightarrow{EF}}{|\overrightarrow{DB}||\overrightarrow{EF}|}$=$\frac{1}{2}$,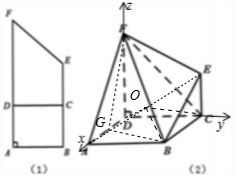
∴異面直線BD與EF所成角為$\frac{π}{3}$.
(2)$G(\frac{1}{2},0,0)$,
設平面$\overrightarrow{BEF}$的法向量為$\overrightarrow{{n}_{1}}$=(x,y,z),
$\overrightarrow{BF}$=(1,1,-2),$\overrightarrow{GF}$=$(-\frac{1}{2},0,2)$.
∴$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{BF}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{GF}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}{x+y-2z=0}\\{-\frac{1}{2}x+2z=0}\end{array}\right.$,
取平面GBF的法向量$\overrightarrow{{n}_{1}}$=(4,-2,1),
同理可得平面BEF的法向量$\overrightarrow{n_1}=(1,1,1)$.
cos$<\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}>$=$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$=$\frac{\sqrt{7}}{7}$.
∵二面角G-BF-C與兩向量的夾角互補,
∴二面角G-BF-C的余弦值為:$-\frac{{\sqrt{7}}}{7}$.
(3)連接AE,取中點為O,連接OA,OB,OC,OD,OE,
由已知易得OA=OB=OC=OD=OE,∴DO長為所求球的半徑.
O$(\frac{1}{2},\frac{1}{2},\frac{1}{2})$,$\overrightarrow{DO}$=$(\frac{1}{2},\frac{1}{2},\frac{1}{2})$,∴r=$|\overrightarrow{DO}|$=$\sqrt{\frac{1}{4}+\frac{1}{4}+\frac{1}{4}}$=$\frac{\sqrt{3}}{2}$.
∴S球的表面積=4πr2=3π.
點評 本題考查了空間位置關系、空間角、法向量的應用、向量夾角公式、球的表面積、直角三角形的性質,考查了推理能力與計算能力,屬于中檔題.


 學習實踐園地系列答案
學習實踐園地系列答案科目:高中數學 來源: 題型:選擇題
| A. | 100° | B. | 160° | C. | 100°或160° | D. | 130° |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $[{\frac{2}{3},+∞})$ | B. | $({\frac{2}{3},+∞})$ | C. | $[{-\frac{1}{12},+∞})$ | D. | $({-\frac{1}{12},+∞})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若長方體的長、寬、高各不相同,則長方體的三視圖中不可能有正方形(以長×寬所在的平面為主視面) | |
| B. | 照片是三視圖中的一種 | |
| C. | 若三視圖中有圓,則原幾何體中一定有球體 | |
| D. | 圓錐的三視圖都是等腰三角形 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x2+y2=3 | B. | y=$\sqrt{1-{x}^{2}}$ | C. | x2+2xy=1(x≠±1) | D. | x2+y2=9(x≠0) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com