
已知定義在![]() 上的奇函數
上的奇函數![]() 在
在![]() 處取得極值.
處取得極值.
(Ⅰ)求函數![]() 的解析式;
的解析式;
(Ⅱ)試證:對于區間![]() 上任意兩個自變量的值
上任意兩個自變量的值![]() ,都有
,都有![]() 成立;
成立;
(Ⅲ)若過點![]() 可作曲線
可作曲線![]() 的三條切線,試求點P對應平面區域的面積.
的三條切線,試求點P對應平面區域的面積.
(Ⅰ) ![]() (Ⅲ)8
(Ⅲ)8
(I)由題意![]() ,∴
,∴![]() ,
,
∴![]() ,又
,又![]() ,
,
即![]()
解得![]() .
.
∴![]() ------------------------------------------------4分
------------------------------------------------4分
(II)∵![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,故
,故![]() 在區間[-1,1]上為減函數,
在區間[-1,1]上為減函數,
∴![]()
對于區間[-1,1]上任意兩個自變量的值![]() ,
,
∴![]() -------------------------------9分
-------------------------------9分
(III)設切點為![]() ,則點M的坐標滿足
,則點M的坐標滿足![]()
因![]() ,故切線
,故切線![]() 的方程為:
的方程為:
![]() ,
,
∵![]() ,∴
,∴![]()
整理得![]() .
.
∵若過點![]() 可作曲線
可作曲線![]() 的三條切線,
的三條切線,
∴關于![]() 方程
方程![]() 有三個實根.
有三個實根.
設![]() ,則
,則
![]() ,
,
由![]() ,得
,得![]() 或
或![]() .
.
由對稱性,先考慮![]()
∵![]() 在
在![]() ,
,![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
∴函數![]() 的極值點為
的極值點為![]() ,或
,或![]()
∴關于![]() 方程
方程![]() 有三個實根的充要條件是
有三個實根的充要條件是
![]() ,解得
,解得![]() .
.
故![]() 時,點P對應平面區域的面積
時,點P對應平面區域的面積![]()
故![]() 時,所求點P對應平面區域的面積為
時,所求點P對應平面區域的面積為![]() ,即8.
,即8.


 名師點撥卷系列答案
名師點撥卷系列答案 英才計劃期末調研系列答案
英才計劃期末調研系列答案科目:高中數學 來源: 題型:
A、(
| ||
B、(
| ||
C、[1,
| ||
D、(-∞,
|
查看答案和解析>>
科目:高中數學 來源:2010年新課標版廣東省遂溪縣高一數學必修一(函數、導數、方程與不等式)單元測試 題型:解答題
已知定義在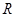 上的奇函數
上的奇函數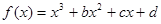 在
在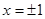 處取得極值.
處取得極值.
(Ⅰ)求函數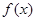 的解析式;
的解析式;
(Ⅱ)試證:對于區間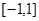 上任意兩個自變量的值
上任意兩個自變量的值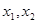 ,都有
,都有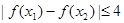 成立;
成立;
(Ⅲ)若過點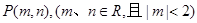 可作曲線
可作曲線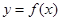 的三條切線,試求點P對應平面區域的面積.
的三條切線,試求點P對應平面區域的面積.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
A.(
| B.(
| C.[1,
| D.(-∞,
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com