
已知函數
 .
.
(1)求函數 的單調遞增區間;
的單調遞增區間;
(2)若對任意 ,函數
,函數 在
在 上都有三個零點,求實數
上都有三個零點,求實數 的取值范圍.
的取值范圍.
(1)詳見解析;(2)實數 的取值范圍是
的取值范圍是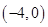 .
.
解析試題分析:(1)求出導數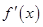 ,并求出導數的零點
,并求出導數的零點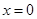 與
與 ,就兩零點的大小進行分類討論,從而得到在相應條件下函數
,就兩零點的大小進行分類討論,從而得到在相應條件下函數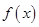 的單調遞增區間;(2)利用(1)中結論,將函數
的單調遞增區間;(2)利用(1)中結論,將函數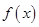 在
在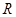 上有三個零點這一條件等價轉化為
上有三個零點這一條件等價轉化為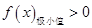 和
和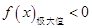 同時成立,列出相應的不等式,利用參數
同時成立,列出相應的不等式,利用參數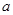 的取值范圍,將
的取值范圍,將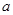 視為相應的自變量,轉化以
視為相應的自變量,轉化以 為參數的不等式,結合恒成立的思想求出參數
為參數的不等式,結合恒成立的思想求出參數 的取值范圍.
的取值范圍.
試題解析:(1)∵ ,∴
,∴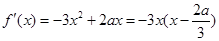 .
.
當 時,
時,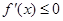 函數
函數 沒有單調遞增區間;
沒有單調遞增區間;
當 時,令
時,令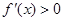 ,得
,得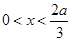 .函數
.函數 的單調遞增區間為
的單調遞增區間為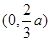 ;
;
當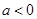 時,令
時,令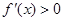 ,得
,得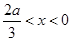 . ,函數
. ,函數 的單調遞增區間為
的單調遞增區間為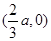 . …6分
. …6分
(2)由(1)知,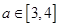 時,
時,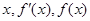 的取值變化情況如下:
的取值變化情況如下: