【題目】已知橢圓
過點
，右焦點
是拋物線
的焦點.
（1）求橢圓
的方程；
（2）已知動直線
過右焦點，且與橢圓分別交于
，
兩點.試問
軸上是否存在定點
，使得
恒成立?若存在求出點的坐標:若不存在，說明理由.
【答案】(1) 
(2)見解析
【解析】
(1) 由橢圓
過點
，得
，由拋物線的焦點為
，得
，利用
即可求解a則方程可求；（2）假設在
軸上存在定點
，當直線
的斜率不存在時，由
，解得
或
；當直線的斜率為0時，由
，解得
或，可得，得點
的坐標為
.再證明當時
恒成立. 設直線的斜率存在且不為0時，其方程為
，與橢圓聯立消去y得韋達定理,向量坐標化得
整理代入韋達定理即可
（1）因為橢圓過點，所以，
又拋物線的焦點為，所以.
所以，解得
（舍去）或
.
所以橢圓的方程為.
（2）假設在軸上存在定點，使得.
①當直線的斜率不存在時，則
，
，
，
，
由，解得或；
②當直線的斜率為0時，則
，
，
，
，
由，解得或.
由①②可得，即點的坐標為.
下面證明當時，恒成立.
當直線的斜率不存在或斜率為0時，由①②知結論成立.
當直線的斜率存在且不為0時，設其方程為，
，
.直線與橢圓聯立得
，
直線經過橢圓內一點，一定與橢圓有兩個交點，且
，
.
，
所以
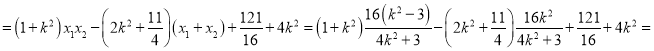
恒成立
綜上所述，在軸上存在點
，使得恒成立.
科目：高中數學 來源： 題型：
【題目】四色猜想是世界三大數學猜想之一，1976年數學家阿佩爾與哈肯證明，稱為四色定理.其內容是：“任意一張平面地圖只用四種顏色就能使具有共同邊界的國家涂上不同的顏色.”用數學語言表示為“將平面任意地細分為不相重疊的區域，每一個區域總可以用1，2，3，4四個數字之一標記，而不會使相鄰的兩個區域得到相同的數字.”如圖，網格紙上小正方形的邊長為1，粗實線圍城的各區域上分別標有數字1，2，3，4的四色地圖符合四色定理，區域
和區域
標記的數字丟失.若在該四色地圖上隨機取一點，則恰好取在標記為1的區域的概率所有可能值中，最大的是______.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若函數
和
同時在
處取得極小值，則稱
和
為一對“
函數”.
（1）試判斷
與
是否是一對“
函數”；
（2）若
與
是一對“函數”.
①求
和
的值；
②當
時，若對于任意
，恒有
，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，圓
的參數方程為
（
為參數），以
為極點，
軸的非負半軸為極軸建立極坐標系，直線
的極坐標方程為
．
（1）求的極坐標方程和直線的直角坐標方程；
（2）射線
與圓的交點為，
，與直線的交點為
，求
的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
