
【題目】已知拋物線![]() 的焦點為
的焦點為![]() ,點
,點![]() 在拋物線
在拋物線![]() 上,
上,![]() ,直線
,直線![]() 過點
過點![]() ,且與拋物線
,且與拋物線![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
(1)求拋物線![]() 的方程及點
的方程及點![]() 的坐標;
的坐標;
(2)求![]() 的最大值.
的最大值.
【答案】(1)![]() ,
,![]() ;(2)9.
;(2)9.
【解析】
(1)根據拋物線上的點到焦點和準線的距離相等,可得p值,即可求拋物線C的方程從而可得解;
(2)設直線l的方程為:x+my﹣1=0,代入y2=4x,得,y2+4my﹣4=0,設A(x1,y1),B(x2,y2),則y1+y2=﹣4m,y1y2=﹣4,x1+x2=2+4m2,x1x2=1,![]() (
(![]() ),
),![]() (x2﹣2,
(x2﹣2,![]() ),由此能求出
),由此能求出![]() 的最大值.
的最大值.
(1)∵點F是拋物線y2=2px(p>0)的焦點,P(2,y0)是拋物線上一點,|PF|=3,
∴2![]() 3,
3,
解得:p=2,
∴拋物線C的方程為y2=4x,
∵點P(2,n)(n>0)在拋物線C上,
∴n2=4×2=8,
由n>0,得n=2![]() ,∴P(2,2
,∴P(2,2![]() ).
).
(2)∵F(1,0),∴設直線l的方程為:x+my﹣1=0,
代入y2=4x,整理得,y2+4my﹣4=0
設A(x1,y1),B(x2,y2),
則y1,y2是y2+4my﹣4=0的兩個不同實根,
∴y1+y2=﹣4m,y1y2=﹣4,
x1+x2=(1﹣my1)+(1﹣my2)=2﹣m(y1+y2)=2+4m2,
x1x2=(1﹣my1)(1﹣my2)=1﹣m(y1+y2)+m2y1y2=1+4m2﹣4m2=1,
![]() (
(![]() ),
),![]() (x2﹣2,
(x2﹣2,![]() ),
),
![]() (x1﹣2)(x2﹣2)+(
(x1﹣2)(x2﹣2)+(![]() )(
)(![]() )
)
=x1x2﹣2(x1+x2)+4![]()
=1﹣4﹣8m2+4﹣4+8![]() m+8
m+8
=﹣8m2+8![]() m+5
m+5
=﹣8(m![]() )2+9.
)2+9.
∴當m![]() 時,
時,![]() 取最大值9.
取最大值9.


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案科目:高中數學 來源: 題型:
【題目】已知拋物線的頂點在原點,過點A(-4,4)且焦點在x軸.
(1)求拋物線方程;
(2)直線l過定點B(-1,0)與該拋物線相交所得弦長為8,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,過點
,過點![]() 的直線
的直線![]() 的參數方程為
的參數方程為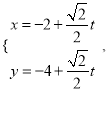 (
(![]() 為參數),直線
為參數),直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點.
兩點.
(Ⅰ)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(Ⅱ)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為梯形,
為梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求證:平面![]()
![]() 平面
平面![]() ;
;
(2)設![]() 為
為![]() 上的一點,滿足
上的一點,滿足![]() ,若直線
,若直線![]() 與平面
與平面![]() 所成角的正切值為
所成角的正切值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一名同學家開了一個小賣部,他為了研究氣溫對某種引領銷售的影響,記錄了2015年7月至12月每月15號下午14時的氣溫和當天的飲料杯數,得到如下資料:

該同學確定的研究方案是:現從這六組數據中選取2組,用剩下的4組數據取線性回歸方程,再用被選中的2組數據進行檢驗.
(1)求選取2組數據恰好是相鄰兩個月的概率;
(2)若選中的是8月與12月的兩組數據,根據剩下的4組數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)若有線性回歸方程得到估計,數據與所宣稱的檢驗數據的誤差不超過3杯,則認為得到的線性回歸方程是理想的,請問(2)所得線性回歸方程是否理想.
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘法估計分別為:
的斜率和截距的最小二乘法估計分別為: 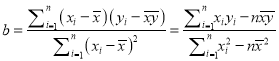 ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層燈數的2倍,則塔的頂層共有燈( )
A. 1盞 B. 3盞 C. 5盞 D. 9盞
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com