
| A. | (-∞,$\frac{\sqrt{3}}{3}$) | B. | (-∞,$\frac{\sqrt{3}}{3}$] | C. | (-∞,-$\frac{\sqrt{3}}{3}$) | D. | (-∞,-$\frac{\sqrt{3}}{3}$] |
分析 求出函數f(x)的導數,得到|$\frac{2y}{\sqrt{1{+y}^{2}}}$|≤1,根據函數的單調性求出a的范圍即可.
解答 解:f′(x)=2a-acosx-sinx,
由f′(x)≤0得,a≤$\frac{sinx}{2-cosx}$,
令y=$\frac{sinx}{2-cosx}$,則2y-ycosx=sinx,
∴2y=$\sqrt{1{+y}^{2}}$sin(x+θ),
∴sin(x+θ)=$\frac{2y}{\sqrt{1{+y}^{2}}}$,
∵|sin(x+θ)|≤1,
∴|$\frac{2y}{\sqrt{1{+y}^{2}}}$|≤1,解得:-$\frac{\sqrt{3}}{3}$≤y≤$\frac{\sqrt{3}}{3}$,
∵函數f(x)在R遞減,
∴a≤ymin=-$\frac{\sqrt{3}}{3}$,
故選:D.
點評 本題考查了函數的單調性、最值問題,考查導數的應用,是一道中檔題.


 培優口算題卡系列答案
培優口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案 A加金題 系列答案
A加金題 系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
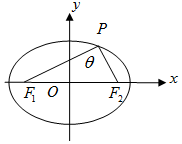 橢圓$\frac{x^2}{4}+{y^2}$=1上的一點P與兩焦點F1,F2所構成的三角形稱為焦點三角形.
橢圓$\frac{x^2}{4}+{y^2}$=1上的一點P與兩焦點F1,F2所構成的三角形稱為焦點三角形.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $3-2\sqrt{2}$ | B. | $2-\sqrt{2}$ | C. | $\sqrt{3}-\sqrt{2}$ | D. | $\sqrt{2}-1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充分必要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com