
已知函數 .
.
(1)當a=l時,求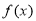 的單調區間;
的單調區間;
(2)若函數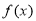 在
在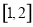 上是減函數,求實數a的取值范圍;
上是減函數,求實數a的取值范圍;
(3)令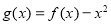 ,是否存在實數a,當
,是否存在實數a,當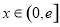 (e是自然對數的底數)時,函數g(x)最小值是3,若存在,求出a的值;若不存在,說明理由.
(e是自然對數的底數)時,函數g(x)最小值是3,若存在,求出a的值;若不存在,說明理由.
(1)單調遞減區間為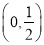 ,單調遞增區間為
,單調遞增區間為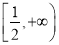 ;(2)
;(2)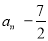 ;(3)存在實數
;(3)存在實數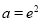 .
.
【解析】
試題分析:(1)把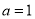 代入函數解析式得
代入函數解析式得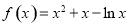 ,且定義域為
,且定義域為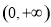 ,利用導數法可求出函數的單調區間,由
,利用導數法可求出函數的單調區間,由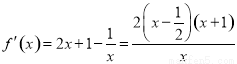 ,分別解不等式
,分別解不等式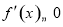 ,
,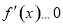 ,注意函數定義域,從而可求出函數
,注意函數定義域,從而可求出函數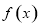 的單調區間;(2)此問題利用導數法來解決,若函數
的單調區間;(2)此問題利用導數法來解決,若函數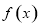 在
在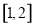 上是減函數,則其導函數
上是減函數,則其導函數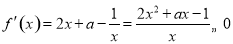 在
在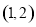 上恒成立,又因為
上恒成立,又因為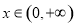 ,所以函數
,所以函數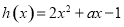 ,必有
,必有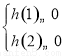 ,從而解得實數
,從而解得實數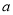 的取值范圍;(3)利用導數求極值的方法來解決此問題,由題意得
的取值范圍;(3)利用導數求極值的方法來解決此問題,由題意得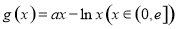 ,則
,則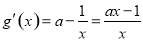 ,令
,令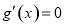 ,解得
,解得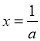 ,通過對
,通過對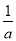 是否在區間
是否在區間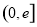 上進行分類討論,可求得當
上進行分類討論,可求得當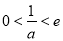 時,有
時,有 ,滿足條件,從而可求出實數
,滿足條件,從而可求出實數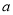 的值.
的值.
(1)當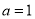 時,
時,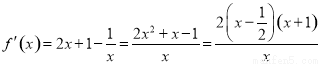 . 2分
. 2分
因為函數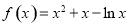 的定義域為
的定義域為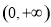 ,
,
所以當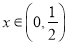 時,
時,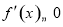 ,當
,當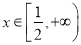 時,
時,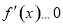 .
.
所以函數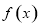 的單調遞減區間為
的單調遞減區間為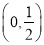 ,單調遞增區間為
,單調遞增區間為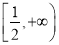 . 4分
. 4分
(2)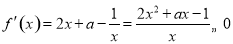 在
在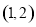 上恒成立.
上恒成立.
令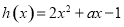 ,有
,有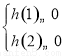 , 6分
, 6分
得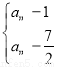 ,
,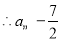 . 8分
. 8分
(3)假設存在實數 ,使
,使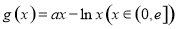 有最小值3,
有最小值3,
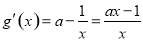 . 9分
. 9分
當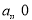 時,
時,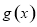 在
在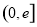 上單調遞減,
上單調遞減,
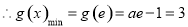 ,
,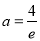 (舍去); 10分
(舍去); 10分
②當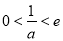 時,
時,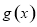 在
在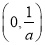 上單調遞減,在
上單調遞減,在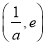 上單調遞增.
上單調遞增.
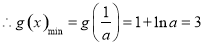 ,解得
,解得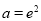 ,滿足條件; 12分
,滿足條件; 12分
③當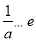 時,
時,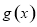 在
在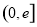 上單調遞減,
上單調遞減,
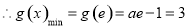 ,
,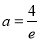 (舍去). 13分
(舍去). 13分
綜上,存在實數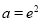 ,使得當
,使得當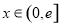 時,
時,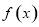 有最小值3. 14分
有最小值3. 14分
考點:1.導數性質;2.不等式求解;3.分類討論.


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:高中數學 來源:2013-2014學年天津市高考5月模擬理科數學試卷(解析版) 題型:選擇題
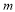 、
、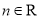 ,
,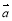 、
、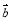 、
、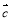 是共起點的向量,
是共起點的向量,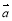 、
、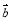 不共線,
不共線,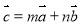 ,則
,則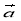 、
、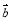 、
、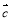 的終點共線的充分必要條件是( )
的終點共線的充分必要條件是( )
A.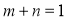 B.
B.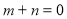 C.
C.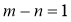 D.
D.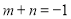
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市紅橋區高三第一次模擬考試文科數學試卷(解析版) 題型:填空題
如圖,AB是半圓O直徑,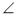 BAC=30o。BC為半圓的切線,且BC=4
BAC=30o。BC為半圓的切線,且BC=4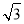 ,則點O到AC的距離OD= .
,則點O到AC的距離OD= .

查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市紅橋區高三第一次模擬考試文科數學試卷(解析版) 題型:選擇題
函數 的部分圖象如圖所示,則
的部分圖象如圖所示,則 的值分別是
的值分別是

A.2,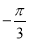 B.2,
B.2, C.4,
C.4, D.4,
D.4,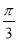
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市河北區高三總復習質量檢測(一)理科數學試卷(解析版) 題型:解答題
己知A、B、C分別為△ABC的三邊a、b、c所對的角,向量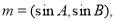
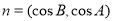 ,且
,且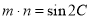 .
.
(1)求角C的大小:
(2)若sinA,sinC,sinB成等差數列,且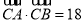 ,求邊c的長.
,求邊c的長.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市河北區高三總復習質量檢測(一)理科數學試卷(解析版) 題型:選擇題
已知函數 ,若
,若 ,且
,且 ,則
,則 的最小值為( ).
的最小值為( ).
(A) (B)
(B) (C)2 (D)4
(C)2 (D)4
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市河北區高三總復習質量檢測(一)文科數學試卷(解析版) 題型:填空題
設F是拋物線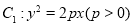 的焦點,點A是拋物線
的焦點,點A是拋物線 與雙曲線
與雙曲線 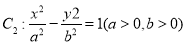 的一條漸近線的一個公共點,且
的一條漸近線的一個公共點,且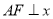 軸,則雙曲線的離心率為_______.
軸,則雙曲線的離心率為_______.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市河東區高三一模試卷文科數學試卷(解析版) 題型:填空題
如圖,AB是圓O的直徑,AD=DE,AB=8,BD=6,則 __________
__________

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com