
【題目】已知數列{an}的前n項和Sn=n2﹣n,數列{bn}的前n項和Tn=4﹣bn .
(1)求數列{an}和{bn}的通項公式;
(2)設cn= ![]() anbn , 求數列{cn}的前n項和Rn的表達式.
anbn , 求數列{cn}的前n項和Rn的表達式.
【答案】
(1)解:∵數列{an}的前n項和Sn=n2﹣n,
∴n=1時,a1=0;
n≥2時,an=Sn﹣Sn﹣1=n2﹣n﹣[(n﹣1)2﹣(n﹣1)]=2n﹣2,
n=1時也成立,
∴an=2n﹣2.
∵數列{bn}的前n項和Tn=4﹣bn,
∴n=1時,b1=4﹣b1,解得b1=2.
n≥2時,bn=Tn﹣Tn﹣1=4﹣bn﹣(4﹣bn﹣1),化為:bn= ![]() .
.
∴數列{bn}是等比數列,首項為2,公比為 ![]() .
.
∴bn= ![]() =
= ![]() .
.
(2)解:cn= ![]() anbn=
anbn= ![]() (2n﹣2)×
(2n﹣2)× ![]() =(n﹣1)×
=(n﹣1)× ![]() .
.
∴數列{cn}的前n項和Rn=0+1+2× ![]() +3×
+3× ![]() +…+(n﹣1)×
+…+(n﹣1)× ![]() .
.
![]() =
= ![]() +2×
+2× ![]() +…+(n﹣2)×
+…+(n﹣2)× ![]() +(n﹣1)×
+(n﹣1)× ![]() ,
,
∴ ![]() Rn=1+
Rn=1+ ![]() +…+
+…+ ![]() ﹣(n﹣1)×
﹣(n﹣1)× ![]() =
= 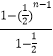 ﹣(n﹣1)×
﹣(n﹣1)× ![]() =2﹣(n+1)×
=2﹣(n+1)× ![]() .
.
∴Rn=4﹣(n+1)× ![]()
【解析】(1)利用遞推關系可得an;利用遞推關系與等比數列的通項公式可得bn . (2)利用“錯位相減法”、等比數列的求和公式即可得出.
【考點精析】解答此題的關鍵在于理解數列的前n項和的相關知識,掌握數列{an}的前n項和sn與通項an的關系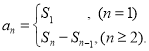 .
.


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(t)= ![]() ,g(x)=cosxf(sinx)﹣sinxf(cosx),x∈(π,
,g(x)=cosxf(sinx)﹣sinxf(cosx),x∈(π, ![]() ).
).
(1)求函數g(x)的值域;
(2)若函數y=|cos(ωx+ ![]() )|f(sin(ωx+
)|f(sin(ωx+ ![]() ))(ω>0)在區間[
))(ω>0)在區間[ ![]() ,π]上為增函數,求實數ω的取值范圍.
,π]上為增函數,求實數ω的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的三個內角A、B、C所對的邊的長分別為a、b、c,設向量 ![]() =(a﹣c,a﹣b),
=(a﹣c,a﹣b), ![]() =(a+b,c),且
=(a+b,c),且 ![]() ∥
∥ ![]() ,
,
(1)求B;
(2)若a=1,b= ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】預計某地區明年從年初開始的前 ![]() 個月內,對某種商品的需求總量
個月內,對某種商品的需求總量 ![]() (萬件)近似滿足:
(萬件)近似滿足: ![]() ,且
,且 ![]() )
)
(1)寫出明年第 ![]() 個月的需求量
個月的需求量 ![]() (萬件)與月份
(萬件)與月份 ![]() 的函數關系式,并求出哪個月份的需求量超過
的函數關系式,并求出哪個月份的需求量超過 ![]() 萬件;
萬件;
(2)如果將該商品每月都投放到該地區 ![]() 萬件(不包含積壓商品),要保證每月都滿足供應,
萬件(不包含積壓商品),要保證每月都滿足供應, ![]() 應至少為多少萬件?(積壓商品轉入下月繼續銷售)
應至少為多少萬件?(積壓商品轉入下月繼續銷售)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】紅隊隊員甲、乙、丙與藍隊隊員A、B、C進行圍棋比賽,甲對A,乙對B,丙對C各一盤,已知甲勝A,乙勝B,丙勝C的概率分別為0.6,0.5,0.5,假設各盤比賽結果相互獨立.
(1)求紅隊至少兩名隊員獲勝的概率;
(2)用ξ表示紅隊隊員獲勝的總盤數,求ξ的分布列和數學期望Eξ.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=Asin(ωx+φ)(其中 ![]() )的圖象如圖所示,為了得到g(x)=sin2x的圖象,則只需將f(x)的圖象( )
)的圖象如圖所示,為了得到g(x)=sin2x的圖象,則只需將f(x)的圖象( ) 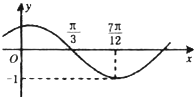
A.向右平移 ![]() 個長度單位
個長度單位
B.向右平移 ![]() 個長度單位
個長度單位
C.向左平移 ![]() 個長度單位
個長度單位
D.向左平移 ![]() 個長度單位
個長度單位
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com