
【題目】設函數![]() .
.
(1)當![]() 時,求
時,求![]() 的極值;
的極值;
(2)當![]() 時,證明:
時,證明: ![]() .
.
【答案】(1)當![]() ,
, ![]() 取得極小值
取得極小值![]() ;當
;當![]() 時,
時, ![]() 取得極大值
取得極大值![]() ;(2)見解析.
;(2)見解析.
【解析】試題分析:(1)當![]() 時,
時, ![]() ,求導
,求導![]() ,然后利用求極值的一般步驟即可得到
,然后利用求極值的一般步驟即可得到![]() 的極值;
的極值;
(2)證明:當![]() 時,
時, ![]() ,
, ![]() ,
,
則證明上述不等式成立,即證明![]() .
.
設![]() ,利用導數研究
,利用導數研究![]() 的性質可得
的性質可得![]() .,
.,
再令![]() ,利用導數研究
,利用導數研究![]() 的性質可得所以
的性質可得所以![]() ,
,
所以![]() ,即
,即![]() .
.
試題解析:(1)當![]() 時,
時, ![]() ,
,
![]()
![]() ,
,
當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上單調遞減;
上單調遞減;
當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上單調遞減.
上單調遞減.
所以,當![]() ,
, ![]() 取得極小值
取得極小值![]() ;
;
當![]() 時,
時, ![]() 取得極大值
取得極大值![]() .
.
(2)證明:當![]() 時,
時, ![]() ,
, ![]() ,
,
所以不等式![]() 可變為
可變為![]() .
.
要證明上述不等式成立,即證明![]() .
.
設![]() ,則
,則![]() ,
,
令![]() ,得
,得![]() ,
,
在![]() 上,
上, ![]() ,
, ![]() 是減函數;在
是減函數;在![]() 上,
上, ![]() ,
, ![]() 是增函數.
是增函數.
所以![]() .
.
令![]() ,則
,則![]() ,
,
在![]() 上,
上, ![]() ,
, ![]() 是增函數;在
是增函數;在![]() 上,
上, ![]() ,
, ![]() 是減函數,
是減函數,
所以![]() ,
,
所以![]() ,即
,即![]() ,即
,即![]() ,
,
由此可知![]() .
.


科目:高中數學 來源: 題型:
【題目】ΔABC的內角A,B,C的對邊分別為a,b,c,根據下列條件解三角形,其中有兩解的是
A. a=2,b=3,A=30°B. b=6,c=4,A=120°
C. a=4![]() ,b=6,A=60°D. a=3,b=6,A=30°
,b=6,A=60°D. a=3,b=6,A=30°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓C: ![]() 的左右焦點分別是F1 , F2 , 離心率為
的左右焦點分別是F1 , F2 , 離心率為 ![]() ,過F1且垂直于x軸的直線被橢圓C截得的線段長為1.
,過F1且垂直于x軸的直線被橢圓C截得的線段長為1.
(1)求橢圓C的方程;
(2)點P是橢圓C上除長軸端點外的任一點,連接PF1 , PF2 , 設∠F1PF2的角平分線PM交C的長軸于點M(m,0),求m的取值范圍;
(3)在(2)的條件下,過點P作斜率為k的直線l,使得l與橢圓C有且只有一個公共點,設直線PF1 , PF2的斜率分別為k1 , k2 , 若k≠0,試證明 ![]() 為定值,并求出這個定值.
為定值,并求出這個定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P-ABC中,∠PAC=∠BAC=90°,PA=PB,點D,F分別為BC,AB的中點.

(1)求證:直線DF∥平面PAC;
(2)求證:PF⊥AD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一組樣本點![]() ,其中
,其中![]() .根據最小二乘法求得的回歸方程是
.根據最小二乘法求得的回歸方程是![]() ,則下列說法正確的是( )
,則下列說法正確的是( )
A. 若所有樣本點都在![]() 上,則變量間的相關系數為1
上,則變量間的相關系數為1
B. 至少有一個樣本點落在回歸直線![]() 上
上
C. 對所有的預報變量![]() ,
,![]() 的值一定與
的值一定與![]() 有誤差
有誤差
D. 若![]() 斜率
斜率![]() ,則變量
,則變量![]() 與
與![]() 正相關
正相關
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等比數列{an}的各項均為正數,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求數列{an}的通項公式;
(2)設bn=log3a1+log3a2+…+log3an,求數列![]() 的前n項和.
的前n項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中以O為極點,x軸正半軸為極軸建立坐標系.圓C1 , 直線C2的極坐標方程分別為ρ=4sinθ,ρcos( ![]() )=2
)=2 ![]() .
.
(1)求C1與C2交點的極坐標;
(2)設P為C1的圓心,Q為C1與C2交點連線的中點,已知直線PQ的參數方程為 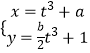 (t∈R為參數),求a,b的值.
(t∈R為參數),求a,b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產一種產品,每年投入固定成本![]() 萬元.此外,每生產
萬元.此外,每生產![]() 件這種產品還需要增加投入
件這種產品還需要增加投入![]() 萬元.經測算,市場對該產品的年需求量為
萬元.經測算,市場對該產品的年需求量為![]() 件,且當出售的這種產品的數量為
件,且當出售的這種產品的數量為![]() (單位:百件)時,銷售所得的收入約為
(單位:百件)時,銷售所得的收入約為![]() (萬元).
(萬元).
(1)若該公司這種產品的年產量為![]() (單位:百件),試把該公司生產并銷售這種產品所得的年利潤
(單位:百件),試把該公司生產并銷售這種產品所得的年利潤![]() 表示為年產量
表示為年產量![]() 的函數;
的函數;
(2)當該公司的年產量![]() 為多少時,當年所得利潤
為多少時,當年所得利潤![]() 最大?最大為多少?
最大?最大為多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com