【題目】在直角坐標系xOy中以O為極點，x軸正半軸為極軸建立坐標系．圓C1 ， 直線C2的極坐標方程分別為ρ=4sinθ，ρcos（ 
）=2 
．
（1）求C1與C2交點的極坐標；
（2）設P為C1的圓心，Q為C1與C2交點連線的中點，已知直線PQ的參數方程為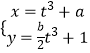 
（t∈R為參數），求a，b的值．
【答案】
（1）解：圓C1，直線C2的直角坐標方程分別為 x2+（y﹣2）2=4，x+y﹣4=0，
解 
得 
或 
，
∴C1與C2交點的極坐標為（4， 
）．（2 
， 
）．
（2）解：由（1）得，P與Q點的坐標分別為（0，2），（1，3），
故直線PQ的直角坐標方程為x﹣y+2=0，
由參數方程可得y= 
x﹣ 
+1，
∴ 
，
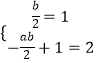解得a=﹣1，b=2．
【解析】（1）先將圓C1 ， 直線C2化成直角坐標方程，再聯立方程組解出它們交點的直角坐標，最后化成極坐標即可；（2）由（1）得，P與Q點的坐標分別為（0，2），（1，3），從而直線PQ的直角坐標方程為x﹣y+2=0，由參數方程可得y= x﹣ +1，從而構造關于a，b的方程組，解得a，b的值．
科目：高中數學 來源： 題型：
【題目】拋物線C1： 
的焦點與雙曲線C2： 
的右焦點的連線交C1于第一象限的點M．若C1在點M處的切線平行于C2的一條漸近線，則p=（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法正確的個數有（ ）
①用
刻畫回歸效果，當
越大時，模型的擬合效果越差；反之，則越好；
②命題“
，
”的否定是“
，
”；
③若回歸直線的斜率估計值是
，樣本點的中心為
，則回歸直線方程是
；
④綜合法證明數學問題是“由因索果”，分析法證明數學問題是“執果索因”。
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
是某港口水的深度
（單位：
）關于時間
的函數，其中
.下表是該港口某一天從
時至
時記錄的時間與水深的關系：
t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y | 5.0 | 7.5 | 5.0 | 2.5 | 5.0 | 7.5 | 5.0 | 2.5 | 5.0 |
經長期觀察，函數的圖像可以近似看成函數
的圖像.最能近似表示表中數據間對應關系的函數是__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，正方體的底面與正四面體的底面在同一平面α上，且AB∥CD，正方體的六個面所在的平面與直線CE，EF相交的平面個數分別記為m，n，那么m+n=（ ） 
A.8
B.9
C.10
D.11
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】動圓M與定圓C：x2＋y2＋4x＝0相外切，且與直線l：x－2＝0相切，則動圓M的圓心的軌跡方程為( )
A. y2－12x＋12＝0 B. y2＋12x－12＝0
C. y2＋8x＝0 D. y2－8x＝0
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系中，直線
的參數方程為
(其中
為參數）.現以坐標原點為極點， 
軸的非負半軸為極軸建立極坐標標系，曲線
的極坐標方程為
.
（1）寫出直線的普通方程和曲線的直角坐標方程；（2）求直線被曲線截得的線段的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
