
 經過
經過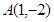 ,
, 兩點,且在兩坐標軸上的四個截距之和為2.
兩點,且在兩坐標軸上的四個截距之和為2. 的方程;
的方程;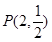 為圓內一點,求經過點
為圓內一點,求經過點 被圓
被圓 截得的弦長最短時的直線
截得的弦長最短時的直線 的方程.
的方程. ;(2)
;(2) .
. ,再令
,再令 、
、 ,分別求出圓在
,分別求出圓在 軸、
軸、 軸上的截距之和,再有已知圓兩坐標軸上的四個截距之和為2.得出
軸上的截距之和,再有已知圓兩坐標軸上的四個截距之和為2.得出 的關系式,由于
的關系式,由于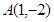 ,
, 兩點在圓上,聯立方程組,解方程組求出系數
兩點在圓上,聯立方程組,解方程組求出系數 ,從而求得圓的方程;(2)考查圓的最短弦,實際上當直線
,從而求得圓的方程;(2)考查圓的最短弦,實際上當直線 過定點
過定點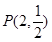 且與過此點的圓的半徑垂直時,
且與過此點的圓的半徑垂直時, 被圓截得的弦長最短,求出直線
被圓截得的弦長最短,求出直線 的斜率,再由直線方程的點斜式求出方程.
的斜率,再由直線方程的點斜式求出方程. 的方程為
的方程為 ,
, ,得
,得 ,則圓在
,則圓在 軸上的截距之和為
軸上的截距之和為 ;
; ,得
,得 ,則圓在
,則圓在 軸上的截距之和為
軸上的截距之和為 ;
; ,即
,即 ,又
,又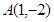 ,
, 兩點在圓上,
兩點在圓上, ,解得
,解得 ,故所求圓
,故所求圓 的方程為
的方程為 .
. 的方程為
的方程為 ,圓心為
,圓心為 ,
, 過定點
過定點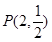 且與過此點的圓的半徑垂直時,
且與過此點的圓的半徑垂直時, 被圓截得的弦長最短,
被圓截得的弦長最短, ,
,
 ,
, 的方程為
的方程為 ,即
,即 .
.

 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com