
【題目】已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的最小正周期是
)的最小正周期是 ![]() ,最小值是﹣2,且圖象經過點(
,最小值是﹣2,且圖象經過點( ![]() ,0),則f(0)= .
,0),則f(0)= .
【答案】![]()
【解析】解:由函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的最小正周期是
)的最小正周期是 ![]() ,最小值是﹣2,
,最小值是﹣2,
可得 ![]() =
= ![]() ,即ω=3,A=2.
,即ω=3,A=2.
再根據f(x)的圖象經過點( ![]() ,0),可得2sin(3×
,0),可得2sin(3× ![]() +φ)=0,可得sin(﹣
+φ)=0,可得sin(﹣ ![]() +φ)=0,∴φ=
+φ)=0,∴φ= ![]() ,f(x)=2sin(3x+
,f(x)=2sin(3x+ ![]() ),
),
故f(0)=2sin ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考點精析】根據題目的已知條件,利用函數y=Asin(ωx+φ)的圖象變換的相關知識可以得到問題的答案,需要掌握圖象上所有點向左(右)平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的橫坐標伸長(縮短)到原來的
的圖象上所有點的橫坐標伸長(縮短)到原來的![]() 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的縱坐標伸長(縮短)到原來的
的圖象上所有點的縱坐標伸長(縮短)到原來的![]() 倍(橫坐標不變),得到函數
倍(橫坐標不變),得到函數![]() 的圖象.
的圖象.


 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:高中數學 來源: 題型:
【題目】隨著手機的發展,“微信”越來越成為人們交流的一種方式.某機構對“使用微信交流”的態度進行調查,隨機抽取了50人,他們年齡的頻數分布及對“使用微信交流”贊成人數如下表.
年齡(單位:歲) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
贊成人數 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年齡45歲為分界點”,由以上統計數據完成下面![]() 列聯表,并判斷是否有99%的把握認為“使用微信交流”的態度與人的年齡有關;
列聯表,并判斷是否有99%的把握認為“使用微信交流”的態度與人的年齡有關;
年齡不低于45歲的人數 | 年齡低于45歲的人數 | 合計 | |
贊成 | |||
不贊成 | |||
合計 |
(Ⅱ)若從年齡在[25,35)和[55,65)的被調查人中按照分層抽樣的方法選取6人進行追蹤調查,并給予其中3人“紅包”獎勵,求3人中至少有1人年齡在[55,65)的概率.
參考數據如下:
附臨界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的觀測值:
的觀測值: ![]() (其中
(其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 為線段
為線段![]() 上的點,
上的點,
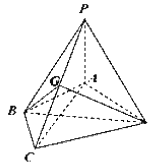
(1)證明: ![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中點,求
的中點,求![]() 與平面
與平面![]() 所成的角的正切值;
所成的角的正切值;
(3)若![]() 滿足
滿足![]() 面
面![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過原點O的圓C,與x軸相交于點A(4,0),與y軸相交于點B(0,2).
(1)求圓C的標準方程;
(2)直線l過B點與圓C相切,求直線l的方程,并化為一般式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函f(x)=sin(ωx+φ)(ω>0,|φ|<π)的部分圖象如圖所示: 
(1)求ω,φ的值;
(2)設g(x)=2 ![]() f(
f( ![]() )f(
)f( ![]() )﹣1,當x∈[0,
)﹣1,當x∈[0, ![]() ]時,求函數g(x)的值域.
]時,求函數g(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】元旦期間,某轎車銷售商為了促銷,給出了兩種優惠方案,顧客只能選擇其中的一種,方案一:每滿![]() 萬元,可減
萬元,可減![]() 千元;方案二:金額超過
千元;方案二:金額超過![]() 萬元(含
萬元(含![]() 萬元),可搖號三次,其規則是依次裝有
萬元),可搖號三次,其規則是依次裝有![]() 個幸運號、
個幸運號、![]() 個吉祥號的一個搖號機,裝有
個吉祥號的一個搖號機,裝有![]() 個幸運號、
個幸運號、![]() 個吉祥號的二號搖號機,裝有
個吉祥號的二號搖號機,裝有![]() 個幸運號、
個幸運號、![]() 個吉祥號的三號搖號機各搖號一次,其優惠情況為:若搖出
個吉祥號的三號搖號機各搖號一次,其優惠情況為:若搖出![]() 個幸運號則打
個幸運號則打![]() 折,若搖出
折,若搖出![]() 個幸運號則打
個幸運號則打![]() 折;若搖出
折;若搖出![]() 個幸運號則打
個幸運號則打![]() 折;若沒有搖出幸運號則不打折.
折;若沒有搖出幸運號則不打折.
(1)若某型號的車正好![]() 萬元,兩個顧客都選中第二中方案,求至少有一名顧客比選擇方案一更優惠的概率;
萬元,兩個顧客都選中第二中方案,求至少有一名顧客比選擇方案一更優惠的概率;
(2)若你評優看中一款價格為![]() 萬的便型轎車,請用所學知識幫助你朋友分析一下應選擇哪種付款方案.
萬的便型轎車,請用所學知識幫助你朋友分析一下應選擇哪種付款方案.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知![]() 是棱長為3的正方體,點
是棱長為3的正方體,點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 上,且
上,且![]() ,(1)求證:
,(1)求證: ![]() 四點共面; (2)若點
四點共面; (2)若點![]() 在
在![]() 上,
上, ![]() ,點
,點![]() 在
在![]() 上,
上, ![]() ,垂足為
,垂足為![]() ,求證:
,求證: ![]() 面
面![]() ; (3)用
; (3)用![]() 表示截面
表示截面![]() 和面
和面![]() 所成銳二面角大小,求
所成銳二面角大小,求![]() .
.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com