
【題目】隨著手機的發展,“微信”越來越成為人們交流的一種方式.某機構對“使用微信交流”的態度進行調查,隨機抽取了50人,他們年齡的頻數分布及對“使用微信交流”贊成人數如下表.
年齡(單位:歲) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
贊成人數 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年齡45歲為分界點”,由以上統計數據完成下面![]() 列聯表,并判斷是否有99%的把握認為“使用微信交流”的態度與人的年齡有關;
列聯表,并判斷是否有99%的把握認為“使用微信交流”的態度與人的年齡有關;
年齡不低于45歲的人數 | 年齡低于45歲的人數 | 合計 | |
贊成 | |||
不贊成 | |||
合計 |
(Ⅱ)若從年齡在[25,35)和[55,65)的被調查人中按照分層抽樣的方法選取6人進行追蹤調查,并給予其中3人“紅包”獎勵,求3人中至少有1人年齡在[55,65)的概率.
參考數據如下:
附臨界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的觀測值:
的觀測值: ![]() (其中
(其中![]() )
)
【答案】(Ⅰ)列聯表見解析,有![]() 的把握認為“使用微信交流”的態度與人的年齡有關;(Ⅱ)
的把握認為“使用微信交流”的態度與人的年齡有關;(Ⅱ)![]() .
.
【解析】試題分析:
(Ⅰ)由所給數據可以計算出年齡不低于45歲和年齡低于45歲的的人中贊成、不贊成的人數,從而可得列聯表,再由所給公式計算![]() 可知有無把握;
可知有無把握;
(Ⅱ)由分層抽樣知區間![]() 上有2人,區間
上有2人,區間![]() 上有4人,把這6人分別編號后,可列舉出任取3人的各種組合,分別計算后可得所求概率.
上有4人,把這6人分別編號后,可列舉出任取3人的各種組合,分別計算后可得所求概率.
試題解析:
(Ⅰ)根據條件得![]() 列聯表:
列聯表:
年齡不低于45歲的人數 | 年齡低于45歲的人數 | 合計 | |
贊成 | 10 | 27 | 37 |
不贊成 | 10 | 3 | 13 |
合計 | 20 | 30 | 50 |
根據列聯表所給的數據代入公式得到:
![]()
所以有![]() 的把握認為“使用微信交流”的態度與人的年齡有關;
的把握認為“使用微信交流”的態度與人的年齡有關;
(Ⅱ)解:
按照分層抽樣方法可知:
[55,65)(歲)抽取:![]() (人);
(人);
[25,35)(歲)抽取:![]() (人)
(人)
解:在上述抽取的6人中, 年齡在[55,65)(歲)有2人,年齡[25,35)(歲)有4人。
年齡在[55,65)(歲)記為![]() ;年齡在[25,35)(歲)記為
;年齡在[25,35)(歲)記為![]() , 則從6人中任取3名的所有情況為:
, 則從6人中任取3名的所有情況為: ![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]()
![]()
![]()
![]() 共20種情況,
共20種情況,
其中至少有一人年齡在[55,65)歲情況有:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共16種情況。
,共16種情況。
記至少有一人年齡在[55,65)歲為事件![]() ,則
,則![]()
∴至少有一人年齡在[55,65)歲之間的概率為![]() .
.


 特高級教師點撥系列答案
特高級教師點撥系列答案科目:高中數學 來源: 題型:
【題目】一家醫藥研究所,從中草藥中提取并合成了甲、乙兩種抗“![]() 病毒”的藥物,經試驗,服用甲、乙兩種藥物痊愈的概率分別為
病毒”的藥物,經試驗,服用甲、乙兩種藥物痊愈的概率分別為![]() .現已進入藥物臨床試用階段,每個試用組由4位該病毒的感染者組成,其中2人試用甲種抗病毒藥物,2人試用乙種抗病毒藥物,如果試用組中,甲種抗病毒藥物治愈人數超過乙種抗病毒藥物的治愈人數,則稱該組為“甲類組”.
.現已進入藥物臨床試用階段,每個試用組由4位該病毒的感染者組成,其中2人試用甲種抗病毒藥物,2人試用乙種抗病毒藥物,如果試用組中,甲種抗病毒藥物治愈人數超過乙種抗病毒藥物的治愈人數,則稱該組為“甲類組”.
(1)求一個試用組為“甲類組”的概率;
(2)觀察3個試用組,用![]() 表示這3個試用組中“甲類組”的個數,求
表示這3個試用組中“甲類組”的個數,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分15分)在直三棱柱![]() 中,底面
中,底面![]() 是邊長為2的正三角形,
是邊長為2的正三角形, ![]() 是棱
是棱![]() 的中點,且
的中點,且![]() .
.
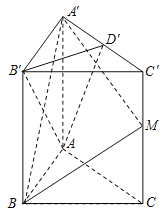
(1)試在棱![]() 上確定一點
上確定一點![]() ,使
,使![]() 平面
平面![]() ;
;
(2)當點![]() 在棱
在棱![]() 中點時,求直線
中點時,求直線![]() 與平面
與平面![]() 所成角的大小的正弦值。
所成角的大小的正弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的一個焦點與拋物線
的一個焦點與拋物線![]() 的焦點
的焦點![]() 重合,且點
重合,且點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
, ![]() 與
與![]() 的公共弦長為
的公共弦長為![]() .
.
(1)求橢圓![]() 的方程及點
的方程及點![]() 的坐標;
的坐標;
(2)過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 兩點,與
兩點,與![]() 交于
交于![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某科技興趣小組對晝夜溫差的大小與小麥新品種發芽多少之間的關系進行了研究,記錄了2016年12月1日至12月5日五天的晝夜溫差與相應每天100顆種子的發芽得到了如下數據:
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
溫差 | 9 | 11 | 10 | 12 | 13 |
發芽數 | 21 | 34 | 26 | 36 | 40 |
現從這5組數據中任選兩組,用余下的三組數據求回歸直線方程,再對被選取的兩組數據進行檢驗.
(Ⅰ)求選取的兩組數據恰好是不相鄰的兩天的概率;
(Ⅱ)若選取的是12月1日和12月5日的兩組數據,請根據余下的三組數據,求出![]() 與
與![]() 的線性回歸直線方程
的線性回歸直線方程![]() ;
;
(Ⅲ)若由線性回歸直線方程得到的估計值與所選出的兩組實際數據的誤差均不超過兩顆,則認為得到的回歸直線方程是可靠的,試判斷(Ⅱ)中得到的線性回歸直線方程是否可靠.
附:在線性回歸方程![]() 中,
中,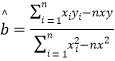 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com