日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
20．設函數$f（x）=\left\{\begin{array}{l}{2^{1-x}}\;，x≤1\\ 1-{log_2}x\;，x＞1\end{array}\right.$，則f[f（-1）]=-1．

分析 由已知中函數$f（x）=\left\{\begin{array}{l}{2^{1-x}}\;，x≤1\\ 1-{log_2}x\;，x＞1\end{array}\right.$，將x=-1代入可得答案．

解答 解：∵函數$f（x）=\left\{\begin{array}{l}{2^{1-x}}\;，x≤1\\ 1-{log_2}x\;，x＞1\end{array}\right.$，
∴f（-1）=4，
f[f（-1）]=f（4）=-1，
故答案為：-1；

點評 本題考查的知識點是分段函數的應用，函數求值，難度不大，屬于基礎題．

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：解答題

6．已知函數f（x）=$\frac{1}{2}a{x^2}$lnx+bx+1．
（1）若曲線y=f（x）在點（1，f（1））處的切線方程為x-2y+1=0，求f（x）的單調區間；
（2）若a=2，且關于x的方程f（x）=1在$[{\frac{1}{e^2}，e}]$上恰有兩個不等的實根，求實數b的取值范圍；
（3）若a=2，b=-1，當x≥1時，關于x的不等式f（x）≥t（x-1）2恒成立，求實數t的取值范圍（其中e是自然對數的底數，e=2，71828…）．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

7．一個車間為了規定工時定額，需要確定加工零件所花費的時間，由此進行了5次實驗，收集數據如下：
零件數：x個1020304050
加工時間：y分鐘5971758189
由以上數據的線性回歸方程估計加工100個零件所花費的時間為（　　）
附：回歸直線的斜率和截距的最小二乘估計公式分別為$\widehatb=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）（{{y_i}-\overline y}）}}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}$，$\widehata=\overline y-\widehatb\overline x$．
A．124分鐘B．150分鐘C．162分鐘D．178分鐘

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

8．已知p：函數f（x）=$\frac{1}{3}$x3-$\frac{1}{2}$ax2+x+b在R上是增函數，q：函數f（x）=xa-2在（0，+∞）上是增函數，則p是￢q的（　　）
A．充分不必要條件B．必要不充分條件
C．充要條件D．既不充分也不必要條件

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

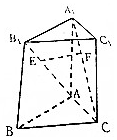15．如圖，在三棱柱ABC-A1B1C1中，已知E，F分別是線段AB1與CA1上的動點，異面直線AB1與CA1所成角為θ，記線段EF中點M的軌邊為L，則|L|等于（　　）
A．$\frac{1}{2}$|AB1|
B．$\sqrt{{\overrightarrow{A{B}_{1}}}^{2}+{\overrightarrow{C{A}_{1}}}^{2}-（\overrightarrow{A{B}_{1}}•\overrightarrow{C{A}_{1}}）^{2}}$
C．$\frac{1}{4}$|AB1|•|CA1|•sinθ
D．$\frac{1}{12}$•V${\;}_{{\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}}$（V${\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$是三棱柱ABC-A1B1C1的體積）

查看答案和解析>>

科目：高中數學 來源： 題型：填空題

5．已知A，B，C是半徑為l的圓O上的三點，AB為圓O的直徑，P為圓O內一點（含圓周），則$\overrightarrow{PA}$$•\overrightarrow{PB}$$+\overrightarrow{PB}$$•\overrightarrow{PC}$$+\overrightarrow{PC}$$•\overrightarrow{PA}$的取值范圍為[-$\frac{4}{3}$，4]．

查看答案和解析>>

科目：高中數學 來源： 題型：填空題

12．設集合A={1，3}，B={a+2，5}，A∩B={3}，則A∪B={1，3，5}．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

9．已知函數$f（x）={e^x}，g（x）=\frac{a}{x}$，a為實常數．
（1）設F（x）=f（x）-g（x），當a＞0時，求函數F（x）的單調區間；
（2）當a=-e時，直線x=m、x=n（m＞0，n＞0）與函數f（x）、g（x）的圖象一共有四個不同的交點，且以此四點為頂點的四邊形恰為平行四邊形．
求證：（m-1）（n-1）＜0．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

10．在銳角三角形ABC 中，角 A，B，C 的對邊分別為 a，b，c．若a=2bsinC，則tanA+tanB+tanC的最小值是（　　）
A．4B．$3\sqrt{3}$C．8D．$6\sqrt{3}$

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 久久精品播放 | 亚洲精品网站在线观看 | 黄色小视频免费看 | 精品视频网站 | 欧美xx孕妇 | 三级在线看 | 日韩精品久久久久久 | 在线视频亚洲 | 91女人18毛片水多国产 | 久久精品欧美一区二区三区不卡 | 国产亚洲久一区二区 | 免费在线观看黄 | 超碰在线观看97 | 久久久精品 | 九九久久精品视频 | 免费高清av | 91网站免费 | 永久免费精品视频 | 久久精品久久久久久久 | 天天射天天舔 | 美女无遮挡网站 | 99热99| 国产精品久久久久久久久久久久久 | 色哟哟精品观看 | 午夜免费视频 | 91久色| 欧美性猛交一区二区三区精品 | 九一国产精品 | av超碰在线 | 亚洲影院在线观看 | 女人av在线 | 国v精品久久久网 | 亚洲欧美精品 | 欧产日产国产69 | 干少妇视频 | 中文字幕激情 | 成人黄色大片 | 精品久久久久久久久久久 | 国产成人毛片 | 国产高潮在线观看 | 视频一二三区 |