Question

4．在四棱錐P-ABCD中，底面ABCD為矩形，平面PAB⊥平面ABCD，AB=AP=3，AD=PB=2，E為線段AB上一點，且AE：EB=7：2，點F，G，M分別為線段PA、PD、BC的中點．
（1）求證：PE⊥平面ABCD；
（2）若平面EFG與直線CD交于點N，求二面角P-MN-A的余弦值．

Answer 1

分析 （1）推導出PE⊥AB，由此能證明PE⊥平面ABCD．…（4分）
（2）以E為坐標原點，EP、EB、EN分別為x軸，y軸，z軸，建立空間直角坐標系，利用向量法能求出二面角P-MN-A的余弦值．

解答 證明：（1）在等腰△APB中，$cos∠ABP=\frac{{\frac{1}{2}PB}}{AB}=\frac{1}{3}$，
則由余弦定理可得$P{E^2}={（\frac{2}{3}）^2}+{2^2}-2×\frac{2}{3}×2×\frac{1}{3}=\frac{32}{9}$，∴$PE=\frac{{4\sqrt{2}}}{3}$．…（2分）
∴PE²+BE²=4=PB²，∴PE⊥AB．…（3分）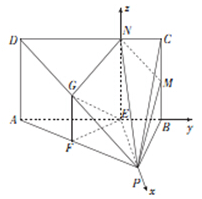
∵平面PAB⊥平面ABCD，平面PAB∩平面ABCD=AB，
∴PE⊥平面ABCD．…（4分）
解：（2）由已知可得EN∥AD，…（5分）
以E為坐標原點，EP、EB、EN分別為x軸，y軸，z軸，建立空間直角坐標系如圖所示，
則$P（\frac{{4\sqrt{2}}}{3}，0，0），M（0，\frac{2}{3}，1），N（0，0，2）$，
從而$\overrightarrow{PM}=（-\frac{{4\sqrt{2}}}{3}，\frac{2}{3}，1）$，$\overrightarrow{MN}=（0，-\frac{2}{3}，1）$．…（7分）
設平面PMN的法向量為$\vec n=（x，y，z）$，則$\vec n•\overrightarrow{PM}=0$，$\vec n•\overrightarrow{MN}=0$，
即$-\frac{{4\sqrt{2}}}{3}x+\frac{2}{3}y+z=0$，$-\frac{2}{3}y+z=0$，
令y=3，可得平面PMN的一個法向量為$\vec n=（\frac{3}{{\sqrt{2}}}，3，2）$．…（9分）
由（1）知平面AMN的一個法向量為$\overrightarrow{EP}=（\frac{{4\sqrt{2}}}{3}，0，0）$，…（10分）
$cos\left?{\vec n，\overrightarrow{EP}}\right＞=\frac{4}{{\frac{{4\sqrt{2}}}{3}×\frac{{\sqrt{35}}}{{\sqrt{2}}}}}=\frac{{3\sqrt{35}}}{35}$，…（11分）
由圖可知二面角P-MN-A的平面角為銳角，
故二面角P-MN-A的余弦值為$\frac{{3\sqrt{35}}}{35}$．…（12分）

點評 本題考查線面垂直的證明，考查二面角的余弦值的求法，是中檔題，解題時要認真審題，注意向量法的合理運用．