
分析 (1)y=$\frac{1}{{2}^{x}+1}$,x≥0,可得$0<y≤\frac{1}{2}$.可得集合A.
(2)對于命題p:?x∈A,使得m≤x成立,可得m$≤\frac{1}{2}$.命題q:函數$f(x)=\frac{m}{x}$在(0,+∞)上單調遞減,可得m>0.p∧q為假命題,p∨q為真命題,可得p與q必然一真一假.
解答 解:(1)∵y=$\frac{1}{{2}^{x}+1}$,x≥0,∴$0<y≤\frac{1}{2}$.A=$(0,\frac{1}{2}]$,
(2)對于命題p:?x∈A,使得m≤x成立,∴m$≤\frac{1}{2}$.
命題q:函數$f(x)=\frac{m}{x}$在(0,+∞)上單調遞減,∴m>0.
∵p∧q為假命題,p∨q為真命題,
p與q必然一真一假.
∴$\left\{\begin{array}{l}{m≤\frac{1}{2}}\\{m≤0}\end{array}\right.$,或$\left\{\begin{array}{l}{m>\frac{1}{2}}\\{m>0}\end{array}\right.$.
解得m≤0,或$m>\frac{1}{2}$.
點評 本題考查了函數的單調性、簡易邏輯的判定方法、不等式的解法,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
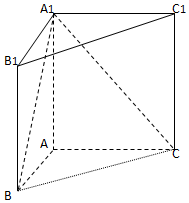 如圖,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.
如圖,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | Y~N(aμ,σ2) | B. | Y~N(0,1) | C. | Y~N($\frac{μ}{a}$,$\frac{σ2}{b}$) | D. | Y~N(aμ+b,a2σ2) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 16 | B. | 28 | C. | 84 | D. | 96 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com