
分析 (1)通過作差可知bn-bn-1=$\frac{{a}_{n}-{a}_{n-1}}{4-2{a}_{n}-2{a}_{n-1}+{a}_{n}{a}_{n-1}}$,結合an-1an-4an-1+4=0可知bn-bn-1=-$\frac{1}{2}$,進而利用數列{bn}是等差數列即可求出通項公式;
(2)通過(1)及bn=bn=$\frac{1}{{2-{a_n}}}(n∈N{\;}^*)$可知an=$\frac{2}{n}$+2,進而可知cn=$\frac{1}{{2}^{n}}$(2n-4),結合單調性可知-1≤cn≤$\frac{1}{4}$,將y=cn+$\frac{1}{2}$t-2t2看作是關于cn的一次函數,結合其單調遞增可知當cn=$\frac{1}{4}$時y≤0即可,進而問題轉化為解不等式$\frac{1}{4}$+$\frac{1}{2}$t-2t2≤0,計算即得結論.
解答 (1)證明:當n≥2時,bn-bn-1=$\frac{1}{2-{a}_{n}}$-$\frac{1}{2-{a}_{n-1}}$=$\frac{{a}_{n}-{a}_{n-1}}{4-2{a}_{n}-2{a}_{n-1}+{a}_{n}{a}_{n-1}}$,
由于an-1an-4an-1+4=0,
所以bn-bn-1=-$\frac{1}{2}$,即數列{bn}是等差數列,
又因為b1=$\frac{1}{2-{a}_{1}}$=-$\frac{1}{2}$,
所以bn=$-\frac{1}{2}$+(n-1)($-\frac{1}{2}$)=-$\frac{n}{2}$;
(2)由(1)及bn=bn=$\frac{1}{{2-{a_n}}}(n∈N{\;}^*)$可知an=$\frac{2}{n}$+2,
所以cn=4bn•(nan-6)=$\frac{1}{{2}^{n}}$(2n-4),
由單調性可知:-1≤cn≤$\frac{1}{4}$,
令y=cn+$\frac{1}{2}$t-2t2,則y是關于cn的一次函數,且單調遞增,
所以當cn=$\frac{1}{4}$時y≤0即可,
所以$\frac{1}{4}$+$\frac{1}{2}$t-2t2≤0,解得:t≤-$\frac{1}{4}$或t≥$\frac{1}{2}$,
故實數t的取值范圍是:(-∞,-$\frac{1}{4}$]∪[$\frac{1}{2}$,+∞).
點評 本題是一道關于數列與不等式的綜合題,考查求數列的通項及前n項和,考查運算求解能力,考查函數思想,注意解題方法的積累,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $({\sqrt{5},2\sqrt{5}})$ | B. | $({2\sqrt{5},5})$ | C. | $({\sqrt{5},5})$ | D. | $({2,\sqrt{5}})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
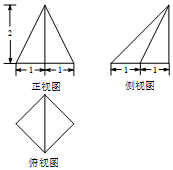
| A. | 2 | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖,網格紙上小正方形的邊長為1,粗實線畫出的是某多面體的三視圖,則該多面體的外接球的表面積等于( )
如圖,網格紙上小正方形的邊長為1,粗實線畫出的是某多面體的三視圖,則該多面體的外接球的表面積等于( )| A. | $4\sqrt{3}π$ | B. | 3π | C. | 8π | D. | 12π |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
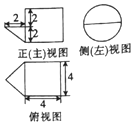
| A. | 6π | B. | $\frac{46}{3}$π | C. | 18π | D. | $\frac{52}{3}$π |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com