
【題目】設函數f(x)在R上存在導數![]() ,有
,有![]() ,在
,在![]() 上,
上,![]() ,若
,若![]() ,則實數m的取值范圍為( )
,則實數m的取值范圍為( )
A.![]() B.
B.![]()
C.[-3,3]D.![]()
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】給出下列命題:①在圓柱的上、下底面的圓周上各取一點,則這兩點的連線是圓柱的母線;②存在每個面都是直角三角形的四面體;③若三棱錐的三條側棱兩兩垂直,則其三個側面也兩兩垂直;④棱臺的上、下底面可以不相似,但側棱長一定相等.其中正確命題的個數是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為評估設備![]() 生產某種零件的性能,從設備
生產某種零件的性能,從設備![]() 生產該零件的流水線上隨機抽取100個零件為樣本,測量其直徑后,整理得到下表:
生產該零件的流水線上隨機抽取100個零件為樣本,測量其直徑后,整理得到下表:
直徑/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | |
件數 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | |
直徑/mm | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合計 |
件數 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
經計算,樣本的平均值![]() ,標準差
,標準差![]() ,以頻率值作為概率的估計值.
,以頻率值作為概率的估計值.
(I)為評判一臺設備的性能,從該設備加工的零件中任意抽取一件,記其直徑為![]() ,并根據以下不等式進行判定(
,并根據以下不等式進行判定(![]() 表示相應事件的概率):①
表示相應事件的概率):①![]() ;②
;②![]() ;③
;③![]() .判定規則為:若同時滿足上述三個式子,則設備等級為甲;若僅滿足其中兩個,則等級為乙;若僅滿足其中一個,則等級為丙;若全部都不滿足,則等級為丁.試判斷設備
.判定規則為:若同時滿足上述三個式子,則設備等級為甲;若僅滿足其中兩個,則等級為乙;若僅滿足其中一個,則等級為丙;若全部都不滿足,則等級為丁.試判斷設備![]() 的性能等級.
的性能等級.
(Ⅱ)將直徑尺寸在![]() 之外的零件認定為是“次品”,將直徑尺寸在
之外的零件認定為是“次品”,將直徑尺寸在![]() 之外的零件認定為“突變品”.從樣本的“次品”中隨意抽取兩件,求至少有一件“突變品”的概率.
之外的零件認定為“突變品”.從樣本的“次品”中隨意抽取兩件,求至少有一件“突變品”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】趙爽是我國古代數學家、天文學家大約在公元222年趙爽為《周碑算經》一書作序時,介紹了“勾股圓方圖”,亦稱“趙爽弦圖”(以弦為邊長得到的正方形是由4個全等的直角三角形再加上中間的一個小正方形組成的)類比“趙爽弦圖”,趙爽弦圖可類似地構造如圖所示的圖形,它是由個3全等的等邊三角形與中間的一個小等邊三角形組成的一個大等邊三角形,設DF2AF,若在大等邊三角形中隨機取一點,則此點取自小等邊三角形的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖①,利用斜二側畫法得到水平放置的![]() 的直觀圖
的直觀圖![]() ,其中
,其中![]() 軸,
軸,![]() 軸.若
軸.若![]() ,設
,設![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,記
,記![]() ,執行如圖②的框圖,則輸出
,執行如圖②的框圖,則輸出![]() 的值
的值
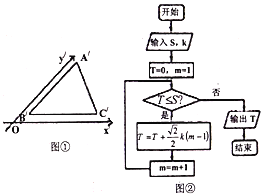
A. 12B. 10C. 9D. 6
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的頂點為原點,其焦點
的頂點為原點,其焦點![]() 到直線
到直線![]() 的距離為
的距離為![]() .設
.設![]() 為直線
為直線![]() 上的點,過點
上的點,過點![]() 作拋物線
作拋物線![]() 的兩條切線
的兩條切線![]() ,其中
,其中![]() 為切點.
為切點.
(1) 求拋物線![]() 的方程;
的方程;
(2) 當點![]() 為直線
為直線![]() 上的定點時,求直線
上的定點時,求直線![]() 的方程;
的方程;
(3) 當點![]() 在直線
在直線![]() 上移動時,求
上移動時,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠![]() ,
,![]() 兩條生產線生產同款產品,若產品按照一、二、三等級分類,則每件可分別獲利10元、8元、6元,現從
兩條生產線生產同款產品,若產品按照一、二、三等級分類,則每件可分別獲利10元、8元、6元,現從![]() ,
,![]() 生產線的產品中各隨機抽取100件進行檢測,結果統計如下圖:
生產線的產品中各隨機抽取100件進行檢測,結果統計如下圖:
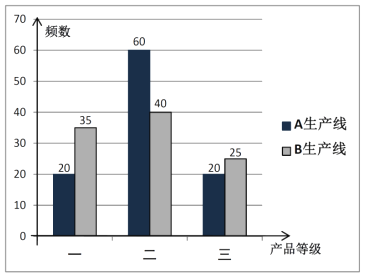
(1)根據已知數據,判斷是否有99%的把握認為一等級產品與生產線有關?
(2)分別計算兩條生產線抽樣產品獲利的方差,以此作為判斷依據,說明哪條生產線的獲利更穩定?
(3)估計該廠產量為2000件產品時的利潤以及一等級產品的利潤.
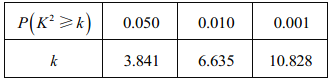
附:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l的參數方程為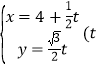 為參數
為參數![]() ,以坐標原點為極點,x軸的正半軸為極軸建建立極坐標系,曲線C的極坐標方程為
,以坐標原點為極點,x軸的正半軸為極軸建建立極坐標系,曲線C的極坐標方程為![]() .
.
![]() 求曲線C的直角坐標方程與直線l的極坐標方程;
求曲線C的直角坐標方程與直線l的極坐標方程;
![]() Ⅱ
Ⅱ![]() 若直線
若直線![]() 與曲線C交于點
與曲線C交于點![]() 不同于原點
不同于原點![]() ,與直線l交于點B,求
,與直線l交于點B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某花店每天以每枝![]() 元的價格從農場購進若干枝玫瑰花,然后以每枝
元的價格從農場購進若干枝玫瑰花,然后以每枝![]() 元的價格出售,如果當天賣不完,剩下的玫瑰花作垃圾處理.
元的價格出售,如果當天賣不完,剩下的玫瑰花作垃圾處理.
(1)若花店一天購進![]() 枝玫瑰花,求當天的利潤
枝玫瑰花,求當天的利潤![]() (單位:元)關于當天需求量
(單位:元)關于當天需求量![]() (單位:枝,
(單位:枝,![]() )的函數解析式.
)的函數解析式.
(2)花店記錄了100天玫瑰花的日需求量(單位:枝),整理得下表:
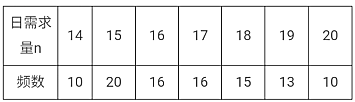
以100天記錄的各需求量的頻率作為各需求量發生的概率.
(i)若花店一天購進![]() 枝玫瑰花,
枝玫瑰花,![]() 表示當天的利潤(單位:元),求
表示當天的利潤(單位:元),求![]() 的分布列,數學期望及方差;
的分布列,數學期望及方差;
(ii)若花店計劃一天購進16枝或17枝玫瑰花,你認為應購進16枝還是17枝?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com