
分析 (1)通過a2=1+d、a5=1+4d,利用a1,a2,a5成等比數列計算可知公差d=2,進而可得結論;
(2)分別利用等差數列、等比數列的求和公式計算,相加即可.
解答 解:(1)依題意可知,a2=1+d,a5=1+4d,
∵a1,a2,a5成等比數列,
∴(1+d)2=1+4d,即d2=2d,
解得:d=2或d=0(舍),
∴an=1+2(n-1)=2n-1;
(2)由(1)可知等差數列{an}的前n項和Pn=$\frac{n(1+2n-1)}{2}$=n2,
∵bn=2n,
∴數列{bn}的前n項和Qn=$\frac{2(1-{2}^{n})}{1-2}$=2n+1-2,
∴Sn=2n+1-n2-2.
點評 本題考查數列的通項及前n項和,考查等差數列、等比數列的求和公式,考查分組求和法,注意解題方法的積累,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 重心 外心 垂心 | B. | 重心 外心 內心 | ||
| C. | 外心 重心 垂心 | D. | 外心 重心 內心 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
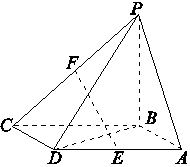 如圖所示,四棱錐P ABCD的底面ABCD是平行四邊形,BD=$\sqrt{2}$,PC=$\sqrt{7}$,PA=$\sqrt{5}$,∠CDP=90°,E、F分別是棱AD、PC的中點.
如圖所示,四棱錐P ABCD的底面ABCD是平行四邊形,BD=$\sqrt{2}$,PC=$\sqrt{7}$,PA=$\sqrt{5}$,∠CDP=90°,E、F分別是棱AD、PC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2n}{n+1}$ | B. | $\frac{2}{n(n+1)}$ | C. | $\frac{n(n+1)}{2}$ | D. | $\frac{n}{2(n+1)}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 班級 | 男生數 | 女生數 | 總數 |
| 高三(1) | 30 | 20 | 50 |
| 高三(2) | 30 | 30 | 60 |
| 高三(3) | 35 | 20 | 55 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com