
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | -3 | C. | 1 | D. | 3 |
分析 將函數f(x)化簡,首先考慮f(x)的單調性,由題意可得f(m)=n,f(n)=m.,故m,n是方程f(x)的同號的相異實數根.利用韋達定理和判別式,求出m,n的關系.在求最大值
解答 解:解:函數$f(x)=\frac{{({a^2}+a)x-1}}{{{a^2}x}}(a∈R,a≠0)$的定義域是{x|x≠0},則[m,n]是其定義域的子集,
∴[m,n]⊆(-∞,0)或(0,+∞).
化簡得f(x)=$\frac{{a}^{2}x+ax-1}{{a}^{2}x}=\frac{1+a}{a}-\frac{1}{{a}^{2}x}$在區間[m,n]上是單調遞增,則有$\left\{\begin{array}{l}{f(n)=m}\\{f(m)=n}\end{array}\right.$,
故m,n是方程f(x)=$\frac{1+a}{a}-\frac{1}{{a}^{2}x}$=x的同號相異的實數根,即m,n是方程(ax)2-(a2+a)x+1=0同號相異的實數根.
那么mn=$\frac{1}{{a}^{2}}$,m+n=$\frac{1+a}{a}$,
只需要△>0,即(a2+a)2-4a2>0,
解得:a>1或a<-3.
那么:n-m=$\sqrt{(n+m)^{2}-4mn}$=$\sqrt{-3(\frac{1}{a}-\frac{1}{3})^{2}+\frac{4}{3}}$,
故n-m的最大值為$\frac{2\sqrt{3}}{3}$,此時解得:a=3.
故選:D.
點評 本題考查了函數性質的方程的運用,有一點綜合性,利用函數關系,構造新的函數解題.屬于中檔題,分類討論思想的運用,增加了本題的難度,解題時注意.


科目:高中數學 來源: 題型:選擇題
| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | asinθ<bsinθ | B. | absinθ<basinθ | ||
| C. | alogbsinθ<blogasinθ | D. | logasinθ<logbsinθ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a<c<b | B. | b<a<c | C. | b<c<a | D. | c<a<b |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
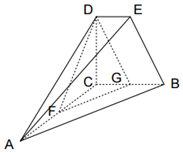 如圖,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分別是AC、BC中點.
如圖,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分別是AC、BC中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com