
【題目】已知函數![]() ,
,![]() .
.
(Ⅰ)求![]() 的反函數的圖象上點(1,0)處的切線方程;
的反函數的圖象上點(1,0)處的切線方程;
(Ⅱ)證明:曲線![]() 與曲線
與曲線![]() 有唯一公共點.
有唯一公共點.
【答案】(1)![]() (2)見解析
(2)見解析
【解析】試題分析:![]() 先求出其反函數,利用導數得出切線的斜率即可
先求出其反函數,利用導數得出切線的斜率即可
![]() 法一:等價函數
法一:等價函數![]() 零點的個數,由
零點的個數,由![]() ,求導
,求導![]() ,再次求導
,再次求導![]() ,判定出單調性,
,判定出單調性,![]() 在
在![]() 上是單調遞增故
上是單調遞增故![]() 在
在![]() 上有唯一的零點 法二:等價于曲線
上有唯一的零點 法二:等價于曲線![]() 與
與![]() 的公共點的個數,當
的公共點的個數,當![]() 時,兩曲線有公共點,求導得函數單調性進行判定
時,兩曲線有公共點,求導得函數單調性進行判定
解析:(Ⅰ)![]() 的反函數為
的反函數為![]() ,設所求切線的斜率為k.
,設所求切線的斜率為k.
∵![]() ,∴
,∴![]() ,于是在點(1,0)處的切線方程為
,于是在點(1,0)處的切線方程為![]() (Ⅱ)證法一:曲線
(Ⅱ)證法一:曲線![]() 與曲線
與曲線![]() 公共點的個數等于函數
公共點的個數等于函數![]() 零點的個數
零點的個數
∵![]() ,∴
,∴![]() 存在零點
存在零點![]() …
…
又![]() ,令
,令![]() ,則
,則![]() .
.
當![]() 時,
時,![]() ,∴
,∴![]() 在
在![]() 上單調遞減;
上單調遞減;
當![]() 時,
時,![]() ,∴
,∴![]() 在
在![]() 上單調遞增,
上單調遞增,
∴![]() 在
在![]() 處有唯一的極小值
處有唯一的極小值![]()
即![]() 在
在![]() 上的最小值為
上的最小值為![]() .
.
∴![]() (當且僅當
(當且僅當![]() 時等號成立),
時等號成立),
∴![]() 在
在![]() 上是單調遞增的,∴
上是單調遞增的,∴![]() 在
在![]() 上有唯一的零點,
上有唯一的零點,
故曲線![]() 與曲線
與曲線![]() 有唯一公共點
有唯一公共點
證法二:∵![]() ,
,![]() ,
,
∴曲線![]() 與曲線
與曲線![]() 公共點的個數等于曲線
公共點的個數等于曲線![]() 與
與![]() 的公共點的個數
的公共點的個數
設![]() ,則
,則![]() ,即當
,即當![]() 時,兩曲線有公共點.
時,兩曲線有公共點.
又![]() (當且僅當
(當且僅當![]() 時等號成立),∴
時等號成立),∴![]() 在
在![]() 上單調遞減,∴
上單調遞減,∴![]() 與
與![]() 有唯一的公共點,
有唯一的公共點,
故曲線![]() 與曲線
與曲線![]() 有唯一公共點
有唯一公共點


科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以直角坐標系的原點
為參數).以直角坐標系的原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立坐標系,曲線
軸的正半軸為極軸建立坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)若過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,與
兩點,與![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,左、右焦點分別為
,左、右焦點分別為![]() 、
、![]() ,過
,過![]() 的直線交橢圓于
的直線交橢圓于![]() 兩點.
兩點.
(1)若以![]() 為直徑的圓內切于圓
為直徑的圓內切于圓![]() ,求橢圓的長軸長;
,求橢圓的長軸長;
(2)當![]() 時,問在
時,問在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() 為定值?并說明理由.
為定值?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年8月20日起,市交警支隊全面啟動路口秩序環境綜合治理,重點整治機動車不禮讓斑馬線和行人的行為,經過一段時間的治理,從市交警隊數據庫中調取了20個路口近三個月的車輛違章數據,經統計得如圖所示的頻率分布直方圖,統計數據中凡違章車次超過30次的設為“重點關注路口”.
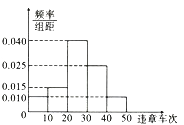
(1)現從“重點關注路口”中隨機抽取兩個路口安排交警去執勤,求抽出來的路口的違章車次一個在![]() ,一個在
,一個在![]() 中的概率;
中的概率;
(2)現從支隊派遣5位交警,每人選擇一個路口執勤,每個路口至多1人,違章車次在![]() 的路口必須有交警去,違章車次在
的路口必須有交警去,違章車次在![]() 的不需要交警過去,設去“重點關注路口”的交警人數為
的不需要交警過去,設去“重點關注路口”的交警人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四棱錐![]() 中,
中,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,BC//AD,已知Q是四邊形ABCD內部一點,且二面角
,BC//AD,已知Q是四邊形ABCD內部一點,且二面角![]() 的平面角大小為
的平面角大小為![]() ,若動點Q的軌跡將ABCD分成面積為
,若動點Q的軌跡將ABCD分成面積為![]() 的兩部分,則
的兩部分,則![]() =_______.
=_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 在平面直角坐標系
在平面直角坐標系![]() 下的參數方程為
下的參數方程為 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系.
軸正半軸為極軸,建立極坐標系.
(1)求曲線![]() 的普通方程及極坐標方程;
的普通方程及極坐標方程;
(2)直線![]() 的極坐標方程是
的極坐標方程是![]() ,射線
,射線![]() :
: ![]() 與曲線
與曲線![]() 交于點
交于點![]() 與直線
與直線![]() 交于點
交于點![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com