
分析 (1)欲求在點(1,f(1))處的切線方程,只須求出其斜率的值即可,故先利用導數求出在x=1處的導函數值,再結合導數的幾何意義即可求出切線的斜率.從而問題解決.
(2)先求導,再構造函數設h(x)=-x2+(2-a)x+a-$\frac{1}{x}$+lnx 由h'(x)在(0,1]上是減函數,可得h'(x)≥h'(1)=2-a,通過研究2-a的正負可判斷h(x)的單調性,進而可得函數F(x)的單調性,可求參數的取值范圍
解答 解:(1)a=2,y=f(x)=x2+2x-lnx,
∴f′(x)=2x+2-$\frac{1}{x}$,
∴f′(1)=2+2-1=3,f(1)=1+2-0=3,
∴曲線在點(1,f(1))處的切線方程為:y-3=3×(x-1),即y=3x.
(2)g(x)=$\frac{f(x)}{{e}^{x}}$,f(x)=x2+ax-lnx,
∴g′(x)=$\frac{-{x}^{2}+(2-a)x+a-\frac{1}{x}+lnx}{{e}^{x}}$,
設h(x)=-x2+(2-a)x+a-$\frac{1}{x}$+lnx,
則h′(x)=-2x+$\frac{1}{{x}^{2}}$+$\frac{1}{x}$+2-a,
易知h′(x)在(0,+∞)上是減函數,
從而h′(x)≥h′(1)=2-a,
①當2-a≥0時,即a≤2時,h′(x)≥0,h(x)在(0,1)上是增函數
∵h(1)=0,
∴h(x)≤0在(0,1]上恒成立,
即g′(x)≤0區間(0,1]上是單調遞減函數,
∴a≤2滿足題意,
②當2-a<0時,即a>2時,設函數h′(x)的唯一零點為x0,則h(x)在(0,x0)上單調遞增,在(x0,1)單調遞減,
又∵h(1)=0,
∴h(x0)>0,
又∵h(e-a)<0,
∴h(x)在(0,1)內有唯一一個零點m,
當x∈(0,m)時,h(x)<0,
當x∈(m,1)時,h(x)>0,從而f(x)在(0,m)上單調遞減,在(m,1)上單調遞增,與在區間(0,1]上是減函數矛盾,
∴a>2不合題意,
綜合所述a的取值范圍為(-∞,2].
點評 考查學生利用導數研究函數的單調能力,函數單調性的判定,以及導數的運算,試題具有一定的綜合性,屬于中檔題.


 出彩同步大試卷系列答案
出彩同步大試卷系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
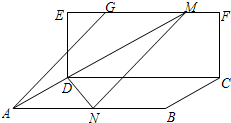 如圖,矩形CDEF所在的平面與矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,點M在線段GF上(包括兩端點),點
如圖,矩形CDEF所在的平面與矩形ABCD所在的平面垂直,AD=$\sqrt{2}$,DE=$\sqrt{3}$,AB=4,EG=$\frac{1}{4}$EF,點M在線段GF上(包括兩端點),點| A. | [30°,45°] | B. | [45°,60°] | C. | [30°,90°) | D. | [60°,90°) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
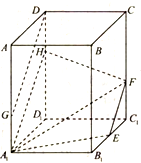 在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E為B1C1的中點,F在CC1上,且C1F=1,G在AA1上,且AG=2.
在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,E為B1C1的中點,F在CC1上,且C1F=1,G在AA1上,且AG=2.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(2a)<f(2)<f(log2a) | B. | f(2)<f(2a)<f(log2a) | C. | f(log2a)<f(2a)<f(2) | D. | f(2)<f(log2a)<f(2a) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $2\sqrt{2}$ | D. | $\frac{{5\sqrt{2}}}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com