Question

如圖所示,已知△ABC是正三角形,PA⊥平面ABC,且PA=AB=a.

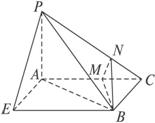
(1)求PB和AC所成的角的大小;

(2)求二面角A-PC-B的大小.

Answer 1

解:如圖所示,

(1)在平面ABC內作BE∥AC,BE=AC,連結AE、PE,則∠PBE是AC和PB所成的角.

∵PA⊥平面ABC,△ABC是正三角形,PA=AB=a,

∴PE=,PB=,EB=a.

在△PEB中,由余弦定理,得cos∠PBE=.

∴∠PBE=arccos,

即PB和AC所成的角的大小為arccos.

(2)取AC的中點M,連結BM,作MN⊥PC于N,連結BN.

∵PA⊥平面ABC,∴平面PAC⊥平面ABC.

易證BM⊥AC,AC=平面PAC∩平面ABC,

∴BM⊥平面PAC.

∵MN⊥PC,∴NB⊥PC.

∴∠MNB是二面角APCB的平面角.

而MN=MC=,BM=,∴tan∠MNB=.

∴∠MNB=arctan,即二面角A-PC-B的大小為arctan.