
【題目】已知函數![]() 是定義在
是定義在![]() 上的奇函數,當
上的奇函數,當![]() 時,
時, .
.
(1)求![]() 在
在![]() 上的解析式;
上的解析式;
(2)若![]() ,函數
,函數![]() ,是否存在實數
,是否存在實數![]() 使得
使得![]() 的最小值為
的最小值為![]() ,若存在,求
,若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
 小學教材全測系列答案
小學教材全測系列答案 小學數學口算題卡脫口而出系列答案
小學數學口算題卡脫口而出系列答案 優秀生應用題卡口算天天練系列答案
優秀生應用題卡口算天天練系列答案 浙江之星課時優化作業系列答案
浙江之星課時優化作業系列答案科目:高中數學 來源: 題型:
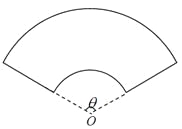
【題目】某單位擬建一個扇環面形狀的花壇(如圖所示),該扇環面是由以點![]() 為圓心的兩個同心圓弧和延長后通過點
為圓心的兩個同心圓弧和延長后通過點![]() 的兩條直線段圍成.按設計要求扇環面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為
的兩條直線段圍成.按設計要求扇環面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為![]() 米,圓心角為
米,圓心角為![]() (弧度).
(弧度).
(1)求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)已知在花壇的邊緣(實線部分)進行裝飾時,直線部分的裝飾費用為4元/米,弧線部分的裝飾費用為9元/米.設花壇的面積與裝飾總費用的比為![]() ,求
,求![]() 關于
關于![]() 的函數關系式,并求出
的函數關系式,并求出![]() 為何值時,
為何值時, ![]() 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在用二次法求方程3x+3x-8=0在(1,2)內近似根的過程中,已經得到f(1)<0,f(1.5)>0,f(1.25)<0,則方程的根落在區間( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不能確定
D. 不能確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在三棱臺![]() 中,點
中,點![]() 在
在![]() 上,且
上,且![]() ,點
,點![]() 是
是![]() 內(含邊界)的一個動點,且有平面
內(含邊界)的一個動點,且有平面![]() 平面
平面![]() ,則動點
,則動點![]() 的軌跡是( )
的軌跡是( )

A. 平面B. 直線C. 線段,但只含1個端點D. 圓
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x|x﹣a|+2x(a∈R).
(1)若函數f(x)在R上單調遞增,求實數a的取值范圍;
(2)若存在實數a∈[﹣4,4]使得關于x的方程f(x)﹣tf(a)=0恰有三個不相等的實數根,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,點
,點![]() 為橢圓
為橢圓![]() 上的動點,若
上的動點,若![]() 的最大值和最小值分別為
的最大值和最小值分別為![]() 和
和![]() .
.
(I)求橢圓![]() 的方程
的方程
(Ⅱ)設不過原點的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,若直線
兩點,若直線![]() 的斜率依次成等比數列,求
的斜率依次成等比數列,求![]() 面積的最大值
面積的最大值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com