
【題目】已知函數f(x)是定義域在R上的奇函數,當x>0時,f(x)=x2﹣2x.
(1)求出函數f(x)在R上的解析式;
(2)寫出函數的單調區間.
【答案】(1)f(x)=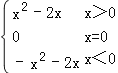 ;
;
(2)則函數的單調遞增區間為為[1,+∞),(﹣∞,﹣1],函數的單調遞減區間為為[﹣1,1].
【解析】
試題(1)根據函數f(x)為定義域為R的奇函數,當x>0時,f(x)=x2﹣2x,我們根據定義域為R的奇函數的圖象必過原點,則f(﹣x)=﹣f(x),即可求出函數f(x)在R上的解析式;
(2)根據(1)中分段函數的解析式,我們易畫出函數f(x)的圖象,利用數形結合進行求解即可.
解:(1)∵函數f(x)是定義域在R上的奇函數,
∴當x=0時,f(0)=0;
當x<0時,﹣x>0,則f(﹣x)=x2+2x.
∵f(x)是奇函數,
∴f(﹣x)=﹣f(x)
∴f(﹣x)=x2+2x=﹣f(x),
即f(x)=﹣x2﹣2x.
綜上:f(x)=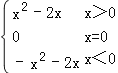 .
.
(2)函數f(x)=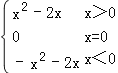 的圖象如下圖所示:
的圖象如下圖所示:
則函數的單調遞增區間為為[1,+∞),(﹣∞,﹣1],
函數的單調遞減區間為為[﹣1,1].
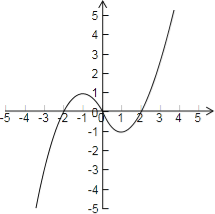


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案科目:高中數學 來源: 題型:
【題目】函數![]() 的圖象為
的圖象為![]() ,則以下結論中正確的是__________.(寫出所有正確結論的編號)
,則以下結論中正確的是__________.(寫出所有正確結論的編號)
①圖象![]() 關于直線
關于直線![]() 對稱;
對稱;
②圖象![]() 關于點
關于點![]() 對稱;
對稱;
③函數![]() 在區間
在區間![]() 內是增函數;
內是增函數;
④由![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度可以得到圖象
個單位長度可以得到圖象![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】由實數組成的集合A具有如下性質:若![]() ,
,![]() 且
且![]() ,那么
,那么![]() .
.
(1)試問集合A能否恰有兩個元素且![]() ?若能,求出所有滿足條件的集合A;若不能,請說明理由;
?若能,求出所有滿足條件的集合A;若不能,請說明理由;
(2)是否存在一個含有元素0的三元素集合A;若存在請求出集合,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 如圖是正方體的平面展開圖.在這個正方體中,
①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.
以上四個命題中,正確命題的序號是________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司在甲、乙兩地銷售某種品牌車,利潤(單位:萬元)分別為![]() 和
和![]() ,其中
,其中![]() 為銷售量(單位:輛)
為銷售量(單位:輛)
(1)當銷售量在什么范圍時,甲地的銷售利潤不低于乙地的銷售利潤;
(2)若該公司在這兩地共銷售![]() 輛車,則甲、乙兩地各銷售多少量時?該公司能獲得利潤
輛車,則甲、乙兩地各銷售多少量時?該公司能獲得利潤![]() 最大,最大利潤是多少?
最大,最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列關于相關系數![]() 的說法不正確的是( )
的說法不正確的是( )
A. 相關系數![]() 越大兩個變量間相關性越強;
越大兩個變量間相關性越強;
B. 相關系數![]() 的取值范圍為
的取值范圍為![]() ;
;
C. 相關系數![]() 時兩個變量正相關,
時兩個變量正相關,![]() 時兩個變量負相關;
時兩個變量負相關;
D. 相關系數![]() 時,樣本點在同一直線上。
時,樣本點在同一直線上。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com