
沒函數 的定義域為R,若存在常數M>0,使
的定義域為R,若存在常數M>0,使 對一切實數x均成 立,則稱
對一切實數x均成 立,則稱 為“倍約束函數”,現給出下列函數:①
為“倍約束函數”,現給出下列函數:① :②
:② :③
:③ ;④
;④ ⑤
⑤ 是定義在實數集R上的奇函數,且
是定義在實數集R上的奇函數,且
對一切 均有
均有 ,其中是“倍約束函數”的有( )
,其中是“倍約束函數”的有( )
A.1個 B.2個 C..3個 D.4個
C
【解析】
試題分析:【解析】
①對于函數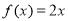 ,存在
,存在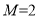 ,使
,使 對 一切實數x均成 立,所以該函數是“倍約束函數”;
對 一切實數x均成 立,所以該函數是“倍約束函數”;
②對于函數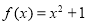 ,當
,當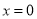 時,
時,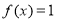 ,故不存在常數M>0,使
,故不存在常數M>0,使 對 一切實數x均成 立,所以該函數不是“倍約束函數”;
對 一切實數x均成 立,所以該函數不是“倍約束函數”;
③對于函數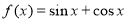 ,當
,當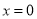 時,
時,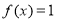 ,故不存在常數M>0,使
,故不存在常數M>0,使 對 一切實數x均成 立,所以該函數不是“倍約束函數”;
對 一切實數x均成 立,所以該函數不是“倍約束函數”;
④對于函數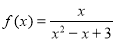 ,因為當
,因為當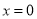 時,
時,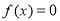 ;
;
當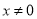 時,
時,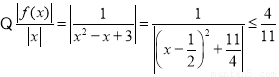 ,所以存在常數
,所以存在常數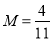 ,使
,使 對 一切實數x均成 立, 所以該函數是“倍約束函數”;
對 一切實數x均成 立, 所以該函數是“倍約束函數”;
⑤由題設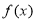 是定義在實數集R上的奇函數,
是定義在實數集R上的奇函數,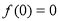 ,所以在
,所以在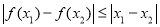 中令
中令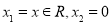 ,于是有
,于是有 ,即存在常數
,即存在常數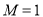 ,使
,使 對 一切實數x均成 立, 所以該函數是“倍約束函數”;
對 一切實數x均成 立, 所以該函數是“倍約束函數”;
綜上可知“倍約束函數”的有①④⑤共三個,所以應選C.
考點:1、新定義;2、賦值法;3、基本初等函數的性質.


 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案 南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案科目:高中數學 來源:2013-2014學年天津市河東區高三一模試卷理科數學試卷(解析版) 題型:解答題
已知函數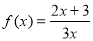 , 數列
, 數列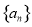 滿足
滿足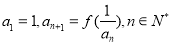 .
.
(1)求數列 的通項公式;
的通項公式;
(2)令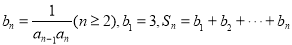 ,若
,若 對一切
對一切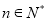 成立,求最小正整數m.
成立,求最小正整數m.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市河東區高三一模理科數學試卷(解析版) 題型:解答題
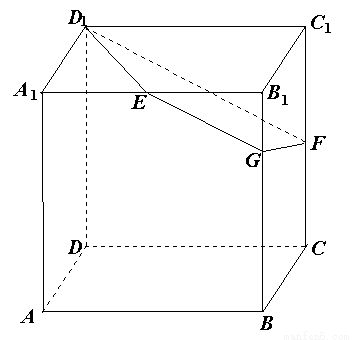
如圖,已知正方體 的棱長為2,E、F分別是
的棱長為2,E、F分別是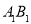 、
、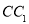 的中點,過
的中點,過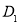 、E、F作平面
、E、F作平面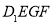 交
交 于G.
于G.
(l)求證:EG∥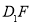 ;
;
(2)求二面角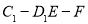 的余弦值;
的余弦值;
(3)求正方體被平面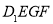 所截得的幾何體
所截得的幾何體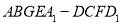 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市河東區高三一模文科數學試卷(解析版) 題型:解答題
已知函數
(1)若函數 的圖象切x軸于點(2,0),求a、b的值;
的圖象切x軸于點(2,0),求a、b的值;
(2)設函數 的圖象上任意一點的切線斜率為k,試求
的圖象上任意一點的切線斜率為k,試求 的充要條件;
的充要條件;
(3)若函數 的圖象上任意不同的兩點的連線的斜率小于l,求證
的圖象上任意不同的兩點的連線的斜率小于l,求證 .
.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市南開區高三第一次模擬考試文科數學試卷(解析版) 題型:選擇題
設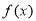 是定義在R上的偶函數,且當
是定義在R上的偶函數,且當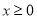 時,
時,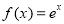 。若對任意的x
。若對任意的x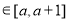 ,不等式
,不等式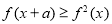 恒成立,則實數a的最大值是( )。
恒成立,則實數a的最大值是( )。
(A)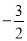 (B)
(B)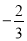 (C)
(C)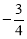 (D)2
(D)2
查看答案和解析>>
科目:高中數學 來源:2013-2014學年四川省高三下學期3月月考文科數學試卷(解析版) 題型:選擇題
執行如圖所示的程序框圖,若輸入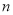 的值為3,則輸出
的值為3,則輸出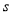 的值是( )
的值是( )

A.1 B.2 C.4 D.7
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com