
分析 (1)${\left.{\overline{2016}}\right|_7}$=6+1×7+2×73=699;
(2)分別求出含有a1、…、an-1,an的項共有m•mn-1(m-1)項及和,即可得出結論.
解答 解:(1)${\left.{\overline{2016}}\right|_7}$=6+1×7+2×73=699;
(2)由題意,a0、a1、…、an-1,各有m種取法,an有m-1中取法.
a0=0,1,2,…m-1時,a1、…、an-1,各有m種取法,an有m-1中取法,
所以含有a0的項共有mn-1(m-1)項,和為(0+1+2+…+m-1)mn-1(m-1)=$\frac{m(m-1)}{2}$mn-1(m-1),
同理a1=0,1,2,…m-1時,a0、a2、…、an-1,各有m種取法,an有m-1中取法,
所以含有a1的項共有m•mn-1(m-1)項,和為(0+1+2+…+m-1)mn-1(m-1)=$\frac{m(m-1)}{2}$m•mn-1(m-1),
…
an=1,2,…m-1時,a0、a1、…、an-1,各有m種取法,
所以含有an的項共有mn•mn項,和為(1+2+…+m-1)mn•mn=$\frac{m(m-1)}{2}$•mn•mn,
所以所有元素之和為$\frac{m(m-1)}{2}$mn-1(m-1)(1+m+…+mn)+$\frac{m(m-1)}{2}$mnmn=$\frac{{({{m^{n+1}}+{m^n}-1})({{m^{n+1}}-{m^n}})}}{2}$.
故答案為:699;$\frac{{({{m^{n+1}}+{m^n}-1})({{m^{n+1}}-{m^n}})}}{2}$.
點評 本題考查新定義,考查數列的求和公式,考查學生分析解決問題的能力,難度大.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
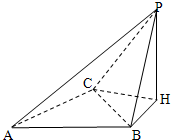 如圖,在四面體P-ABC,底面ABC是邊長為1的正三角形,AB⊥BP,點P在底面ABC上的射影為H,BH=$\frac{\sqrt{3}}{3}$,平面ACP與平面PBH所成的銳二面角的余弦值為$\frac{\sqrt{6}}{3}$.
如圖,在四面體P-ABC,底面ABC是邊長為1的正三角形,AB⊥BP,點P在底面ABC上的射影為H,BH=$\frac{\sqrt{3}}{3}$,平面ACP與平面PBH所成的銳二面角的余弦值為$\frac{\sqrt{6}}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | $\frac{16\sqrt{2}}{3}$cm3 | B. | $\frac{32}{3}$cm3 | C. | 16$\sqrt{2}$cm3 | D. | 32cm3 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
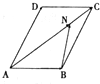
| A. | $\frac{3}{4}\overrightarrow b+\frac{1}{4}\overrightarrow a$ | B. | $\frac{1}{4}\overrightarrow b+\frac{3}{4}\overrightarrow a$ | C. | $\frac{3}{4}\overrightarrow b-\frac{1}{4}\overrightarrow a$ | D. | $\frac{1}{4}\overrightarrow b-\frac{3}{4}\overrightarrow a$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3或-1 | B. | 3 | C. | 1 | D. | -3或1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com