
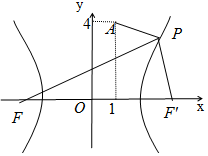
 已知F是雙曲線C:$\frac{x^2}{4}-\frac{y^2}{12}=1$的左焦點,A(1,4),P是雙曲線右支上的動點.求:
已知F是雙曲線C:$\frac{x^2}{4}-\frac{y^2}{12}=1$的左焦點,A(1,4),P是雙曲線右支上的動點.求:分析 (1)設雙曲線的右焦點為F',求出雙曲線的a,b,c,以及焦點坐標,運用雙曲線的定義和三點共線,可得最小值為|AF'|;
(2)延長FA交雙曲線右支于P,由|PF|-|PA|≤|AF|,結合漸近線的斜率和直線AF的斜率的關系,計算即可得到所求最大值.
解答 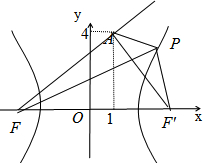 解:(1)設雙曲線的右焦點為F',
解:(1)設雙曲線的右焦點為F',
雙曲線C:$\frac{x^2}{4}-\frac{y^2}{12}=1$的a=2,b=2$\sqrt{3}$,c=$\sqrt{{a}^{2}+{b}^{2}}$=4,
可得F(-4,0),F'(4,0),
由雙曲線的定義可得|PF|-|PF'|=2a=4,
可得|PF|=4+|PF'|,
則|PF|+|PA|=4+|PF'|+|PA|≥|AF'|,當A,P,F'共線時,取得等號.
|AF'|=$\sqrt{(1-4)^{2}+(4-0)^{2}}$=5.
可得|PF|+|PA|的最小值為5;
(2)|PF|-|PA|≤|AF|,當A,P,F三點共線時,取得等號.
延長FA交雙曲線右支于P,由雙曲線的漸近線的斜率為±$\sqrt{3}$,
直線AF的斜率為$\frac{4-0}{1+4}$=$\frac{4}{5}$<$\sqrt{3}$,則P點存在.
|AF|=$\sqrt{(1+4)^{2}+(4-0)^{2}}$=$\sqrt{41}$.
則|PF|-|PA|的最大值為$\sqrt{41}$.
點評 本題考查雙曲線的方程和性質,主要是定義法的運用,以及三點共線取得最值,考查數形結合思想方法,屬于中檔題.


 時刻準備著暑假作業原子能出版社系列答案
時刻準備著暑假作業原子能出版社系列答案 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 20 | B. | 18 | C. | 16 | D. | 14 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | x=-1 | B. | x=0 | C. | $x=\frac{1}{2}$ | D. | $x=-\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
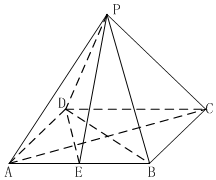 如圖,四棱錐P-ABCD的底面ABCD為矩形,AB=2$\sqrt{2}$,BC=2,點P在底面上的射影在AC上E是AB的中點.
如圖,四棱錐P-ABCD的底面ABCD為矩形,AB=2$\sqrt{2}$,BC=2,點P在底面上的射影在AC上E是AB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com