
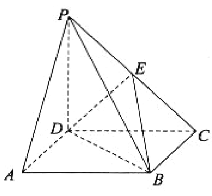
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,
是平行四邊形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一點(diǎn).
上的一點(diǎn).
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,求
,求![]() 的值;
的值;
(3)在(2)的條件下,三棱錐![]() 的體積是18,求
的體積是18,求![]() 點(diǎn)到平面
點(diǎn)到平面![]() 的距離.
的距離.
【答案】(1)見解析 ;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)推導(dǎo)出BC⊥PD,BD⊥BC,由此能證明BC⊥平面PBD.(2)連結(jié)AC,交BD于O,連結(jié)OE,由PA∥平面BDE,得OE∥PA,由此能求出![]() .(3)B到平面PCD的距離d=
.(3)B到平面PCD的距離d=
3![]() ,設(shè)PD=a,則
,設(shè)PD=a,則![]() =
=![]() ,由三棱錐P﹣BDE的體積是18,求出PD=a=6,設(shè)點(diǎn)D到平面PAB的距離為h,由VP﹣ABD=VD﹣PAB,能求出D點(diǎn)到平面PAB的距離.
,由三棱錐P﹣BDE的體積是18,求出PD=a=6,設(shè)點(diǎn)D到平面PAB的距離為h,由VP﹣ABD=VD﹣PAB,能求出D點(diǎn)到平面PAB的距離.
(1)∵在四棱錐P﹣ABCD中,底面ABCD是平行四邊形,PD⊥平面ABCD,
∴BC⊥PD,∵AD=BD=6,AB=6![]() ,BC=AD,∴BD2+BC2=CD2,∴BD⊥BC,
,BC=AD,∴BD2+BC2=CD2,∴BD⊥BC,
∵PD∩BD=D,∴BC⊥平面PBD.
(2)連結(jié)AC交BD于O,連結(jié)OE,則O是AC的中點(diǎn),

∵PA∥平面BDE,∴OE∥PA,∴E是PC的中點(diǎn),∴![]() =
=![]() .
.
(3)B到平面PCD的距離d=![]() =3
=3![]() ,設(shè)PD=a,則
,設(shè)PD=a,則![]() =
=![]()
![]() =
=![]() ,∵三棱錐P﹣BDE的體積是18,∴VP﹣BDE=VB﹣PDE=
,∵三棱錐P﹣BDE的體積是18,∴VP﹣BDE=VB﹣PDE=![]() =
=![]() =18,解得PD=a=6,設(shè)點(diǎn)D到平面PAB的距離為h,
=18,解得PD=a=6,設(shè)點(diǎn)D到平面PAB的距離為h,
∵PD⊥平面ABCD,AD=BD=6,AB=6![]() ,
,
∴PA=PB=![]() =6
=6![]() ,
,
∴![]() =18
=18![]() ,
,
![]() =
=![]() =18,
=18,
∵VP﹣ABD=VD﹣PAB,∴![]() ,
,
∴h=![]() =
=![]() =2
=2![]() .∴D點(diǎn)到平面PAB的距離為2
.∴D點(diǎn)到平面PAB的距離為2![]() .
.


 互動課堂系列答案
互動課堂系列答案 激活思維智能訓(xùn)練課時(shí)導(dǎo)學(xué)練系列答案
激活思維智能訓(xùn)練課時(shí)導(dǎo)學(xué)練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修![]() :不等式選講
:不等式選講
已知函數(shù)f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若關(guān)于x的不等式f(x)≤|3m+1|有解,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 是定義在
是定義在![]() 上的函數(shù),其導(dǎo)函數(shù)為
上的函數(shù),其導(dǎo)函數(shù)為![]() ,若
,若![]() ,
,![]() ,則不等式
,則不等式![]() (其中
(其中![]() 為自然對數(shù)的底數(shù))的解集為______.
為自然對數(shù)的底數(shù))的解集為______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】中國傳統(tǒng)文化中很多內(nèi)容體現(xiàn)了數(shù)學(xué)的對稱美,如圖所示的太極圖是由黑白兩個(gè)魚形紋組成的圓形圖案,充分展現(xiàn)了相互轉(zhuǎn)化、對稱統(tǒng)一的形式美、和諧美,給出定義:能夠?qū)AO的周長和面積同時(shí)平分的函數(shù)稱為這個(gè)圓的“優(yōu)美函數(shù)”,給出下列命題:
①對于任意一個(gè)圓O,其“優(yōu)美函數(shù)”有無數(shù)個(gè);
②函數(shù)f(x)=ln(![]() )可以是某個(gè)圓的“優(yōu)美函數(shù)”;
)可以是某個(gè)圓的“優(yōu)美函數(shù)”;
③函數(shù)y=1+sinx可以同時(shí)是無數(shù)個(gè)圓的“優(yōu)美函數(shù)”;
④函數(shù)y=2x+1可以同時(shí)是無數(shù)個(gè)圓的“優(yōu)美函數(shù)”;
⑤函數(shù)y=f(x)是“優(yōu)美函數(shù)”的充要條件為函數(shù)y=f(x)的圖象是中心對稱圖形.
其中正確的命題是_____.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知,橢圓C過點(diǎn)![]() ,兩個(gè)焦點(diǎn)為
,兩個(gè)焦點(diǎn)為![]() ,
,![]() ,E,F是橢圓C上的兩個(gè)動點(diǎn),如果直線AE的斜率與AF的斜率互為相反數(shù),直線EF的斜率為
,E,F是橢圓C上的兩個(gè)動點(diǎn),如果直線AE的斜率與AF的斜率互為相反數(shù),直線EF的斜率為![]() ,直線l與橢圓C相切于點(diǎn)A,斜率為
,直線l與橢圓C相切于點(diǎn)A,斜率為![]() .
.
![]() 求橢圓C的方程;
求橢圓C的方程;
![]() 求
求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(1)已知直線![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() ,且與直線
,且與直線![]() 的夾角為
的夾角為![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)已知![]() 中頂點(diǎn)
中頂點(diǎn)![]() 的平分線方程分別為
的平分線方程分別為![]() 和
和![]() .求
.求![]() 邊所在的直線方程.
邊所在的直線方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知雙曲線![]() 的一個(gè)焦點(diǎn)是
的一個(gè)焦點(diǎn)是![]() ,且
,且![]()
(1)求雙曲線![]() 的方程
的方程
(2)設(shè)經(jīng)過焦點(diǎn)![]() 的直線
的直線![]() 的一個(gè)法向量為
的一個(gè)法向量為![]() ,當(dāng)直線
,當(dāng)直線![]() 與雙曲線
與雙曲線![]() 的右支相交于不同的兩點(diǎn)
的右支相交于不同的兩點(diǎn)![]() 時(shí),求實(shí)數(shù)
時(shí),求實(shí)數(shù)![]() 的取值范圍
的取值范圍
(3)設(shè)(2)中直線![]() 與雙曲線
與雙曲線![]() 的右支相交于
的右支相交于![]() 兩點(diǎn),問是否存在實(shí)數(shù)
兩點(diǎn),問是否存在實(shí)數(shù)![]() ,使得
,使得![]() 為銳角?若存在,請求出
為銳角?若存在,請求出![]() 的范圍;若不存在,請說明理由
的范圍;若不存在,請說明理由
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com