日韩精品在线视频,国产欧美在线观看,另类天堂av

3．某班級要從4名男生，2名女生中選派4人參加某次社區服務，如果要求至少有1名女生，那么不同的選派方案種數為（　　）

A．

B．

C．

D．

分析法一：用直接法，4人中至少有1名女生包括1女3男及2女2男兩種情況，計算各種情況下的選派方案種數，由加法原理，計算可得答案；
法二：用排除法，首先計算從4男2女中選4人的選派方案種數，再計算4名都是男生的選派方案種數，由排除法，計算可得答案．

解答解：法一：4人中至少有1名女生包括1女3男及2女2男兩種情況，
故不同的選派方案種數為C¹₂•C³₄+C²₂•C²₄=2×4+1×6=14；
法二：從4男2女中選4人共有C⁴₆種選法，4名都是男生的選法有C⁴₄種，
故至少有1名女生的選派方案種數為C⁴₆-C⁴₄=15-1=14．
故選D．

點評本題考查簡單的排列組合，如果分類討論太復雜的題目最好用間接法即排除法，以避免直接的分類不全情況出現．

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：填空題

13．在直角坐標系xOy中，設集合Ω={（x，y）|0≤x≤2，0≤y≤1}，在區域Ω內任取一點P（x，y），則滿足x+y≥1的概率是$\frac{3}{4}$．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

14．

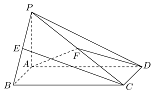如圖，在四棱錐P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PB、PD與
平面ABCD所成的角依次是$\frac{π}{4}$和$arctan\frac{1}{2}$，AP=2，E、F依次是PB、PC的中點；
（1）求異面直線EC與PD所成角的大小；（結果用反三角函數值表示）
（2）求三棱錐P-AFD的體積．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

11．曲線C₁：y=sinx，曲線${C_2}：{x^2}+{（y+r-\frac{1}{2}）^2}={r^2}$（r＞0），它們交點的個數（　　）

A．

恒為偶數

B．

恒為奇數

C．

不超過2017

D．

可超過2017

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

18．已知集合M={（x，y）|y=f（x）}，若對于任意實數對（x₁，y₁）∈M，存在（x₂，y₂）∈M，使x₁x₂+y₁y₂=0成立，則稱集合M是“垂直對點集”．給出下列四個集合：
①M={（x，y）|y=$\frac{1}{{x}^{2}}$}；
②M={（x，y）|y=log₂x}；
③M={（x，y）|y=2^x-2}；
④M={（x，y）|y=sinx+1}．
其中是“垂直對點集”的序號是（　　）

A．

①②③

B．

①②④

C．

①③④

D．

②③④

查看答案和解析>>

科目：高中數學 來源： 題型：填空題

8．集合{x|1＜x＜6，x∈N^*}的非空真子集的個數為14

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

15．下列判斷中正確的是（　　）

	A．	$f（x）={（\sqrt{x}）^2}$是偶函數		B．	$f（x）=\frac{{{x^2}-x}}{x-1}$是奇函數
	C．	$f（x）=\frac{{{2^x}+1}}{{{2^x}-1}}$是偶函數		D．	$f（x）=\frac{{\sqrt{4-{x^2}}}}{\|x-3\|-3}$是奇函數

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

1．設函數f（x）=|x-3|+|x-a|，如果對任意x∈R，f（x）≥4，則a的取值范圍是（　　）

A．

（-∞，-7]∪[1，+∞）

B．

[-7，1]

C．

（-∞，-1]∪[7，+∞）

D．

[-1，7]

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

2．已知點P（-2，3），點Q（-6，-1），則直線PQ的傾斜角為（　　）

A．

30°

B．

45°

C．

60°

D．

135°

查看答案和解析>>

同步練習冊答案

日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

練習冊

高中

初中

小學