
【題目】在直角坐標系xOy中,動點P與定點![]() 的距離和它到定直線
的距離和它到定直線![]() 的距離之比是
的距離之比是![]() ,設動點P的軌跡為E.
,設動點P的軌跡為E.
(1)求動點P的軌跡E的方程;
(2)設過F的直線交軌跡E的弦為AB,過原點的直線交軌跡E的弦為CD,若![]() ,求證:
,求證:![]() 為定值.
為定值.
 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數學 來源: 題型:
【題目】某社會機構為了調查對手機游戲的興趣與年齡的關系,通過問卷調查,整理數據得如下![]() 列聯表:
列聯表:

(1)根據列聯表,能否有99.9%的把握認為對手機游戲的興趣程度與年齡有關?
(2)若已經從40歲以下的被調查者中用分層抽樣的方式抽取了5名,現從這5名被調查者中隨機選取3名,求這3名被調查者中恰有1名對手機游戲無興趣的概率.
附: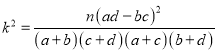
參考數據:

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以坐標原點為極點,
中,以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)![]() 為曲線
為曲線![]() 上的動點,點
上的動點,點![]() 在線段
在線段![]() 上,且滿足
上,且滿足![]() ,求點
,求點![]() 的軌跡
的軌跡![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 的極坐標為
的極坐標為![]() ,點
,點![]() 在曲線
在曲線![]() 上,求
上,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=ax2-a-lnx,其中a ∈R.
(I)討論f(x)的單調性;
(II)確定a的所有可能取值,使得![]() 在區間(1,+∞)內恒成立(e=2.718…為自然對數的底數)。
在區間(1,+∞)內恒成立(e=2.718…為自然對數的底數)。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 九章算術
九章算術![]() 是我國古代著名數學經典
是我國古代著名數學經典![]() 其中對勾股定理的論述比西方早一千多年,其中有這樣一個問題:“今有圓材埋在壁中,不知大小
其中對勾股定理的論述比西方早一千多年,其中有這樣一個問題:“今有圓材埋在壁中,不知大小![]() 以鋸鋸之,深一寸,鋸道長一尺
以鋸鋸之,深一寸,鋸道長一尺![]() 問徑幾何?”其意為:今有一圓柱形木材,埋在墻壁中,不知其大小,用鋸去鋸該材料,鋸口深一寸,鋸道長一尺
問徑幾何?”其意為:今有一圓柱形木材,埋在墻壁中,不知其大小,用鋸去鋸該材料,鋸口深一寸,鋸道長一尺![]() 問這塊圓柱形木料的直徑是多少?長為1丈的圓柱形木材部分鑲嵌在墻體中,截面圖如圖所示
問這塊圓柱形木料的直徑是多少?長為1丈的圓柱形木材部分鑲嵌在墻體中,截面圖如圖所示![]() 陰影部分為鑲嵌在墻體內的部分
陰影部分為鑲嵌在墻體內的部分![]() 已知弦
已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算該木材鑲嵌在墻中的體積約為( )(注:1丈
寸,估算該木材鑲嵌在墻中的體積約為( )(注:1丈![]() 尺
尺![]() 寸,
寸,![]() ,
,![]() )
)

A. 600立方寸 B. 610立方寸 C. 620立方寸 D. 633立方寸
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下四個命題中:①在回歸分析中,可用相關系數r的值判斷模型的擬合效果,|r|越大,模擬的擬合效果越好;②在一組樣本數據![]() 不全相等)的散點圖中,若所有樣本點
不全相等)的散點圖中,若所有樣本點![]() 都在直線
都在直線![]() 上,則這組樣本數據的線性相關系數為
上,則這組樣本數據的線性相關系數為![]() ;③對分類變量x與y的隨機變量
;③對分類變量x與y的隨機變量![]() 來說,
來說,![]() 越小,判斷“x與y有關系”的把握程度越大.其中真命題的個數為__________.
越小,判斷“x與y有關系”的把握程度越大.其中真命題的個數為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年春節期間,我國高速公路繼續執行“節假日高速公路免費政策”.某路橋公司為掌握春節期間車輛出行的高峰情況,在某高速公路收費點記錄了大年初三上午![]() 這一時間段內通過的車輛數,統計發現這一時間段內共有600輛車通過該收費點,它們通過該收費點的時刻的頻率分布直方圖如下圖所示,其中時間段
這一時間段內通過的車輛數,統計發現這一時間段內共有600輛車通過該收費點,它們通過該收費點的時刻的頻率分布直方圖如下圖所示,其中時間段![]() 記作區間
記作區間![]() ,
,![]() 記作
記作![]() ,
,![]() 記作
記作![]() ,
,![]() 記作
記作![]() ,例如:10點04分,記作時刻64.
,例如:10點04分,記作時刻64.
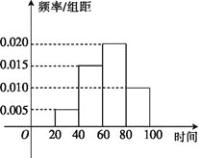
(1)估計這600輛車在![]() 時間段內通過該收費點的時刻的平均值
時間段內通過該收費點的時刻的平均值![]() 同一組中的數據用該組區間的中點值代表
同一組中的數據用該組區間的中點值代表![]() ;
;
(2)為了對數據進行分析,現采用分層抽樣的方法從這600輛車中抽取10輛,再從這10輛車中隨機抽取4輛,設抽到的4輛車中,在![]() 之間通過的車輛數為
之間通過的車輛數為![]() ,求
,求![]() 的分布列與數學期望;
的分布列與數學期望;
(3)由大數據分析可知,車輛在每天通過該收費點的時刻服從正態分布![]() ,其中
,其中![]() 可用這600輛車在
可用這600輛車在![]() 之間通過該收費點的時刻的平均值近似代替,
之間通過該收費點的時刻的平均值近似代替,![]() 可用樣本的方差近似代替
可用樣本的方差近似代替![]() 同一組中的數據用該組區間的中點值代表
同一組中的數據用該組區間的中點值代表![]() ,已知大年初五全天共有1000輛車通過該收費點,估計在
,已知大年初五全天共有1000輛車通過該收費點,估計在![]() 之間通過的車輛數
之間通過的車輛數![]() 結果保留到整數
結果保留到整數![]() .
.
參考數據:若![]() ,則
,則![]() ;
;
![]() ;
;![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是各項均為正數的等比數列,
是各項均為正數的等比數列,![]() 是等差數列,且
是等差數列,且![]() .
.
(I)求![]() 和
和![]() 的通項公式;
的通項公式;
(II)設數列![]() 滿足
滿足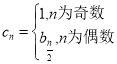 ,求
,求![]() ;
;
(III)對任意正整數![]() ,不等式
,不等式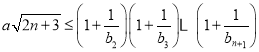 成立,求正數
成立,求正數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,函數f(x)=2cosxsin(x﹣A)+sinA(x∈R)在x=![]() 處取得最大值.
處取得最大值.
(1)當![]() 時,求函數f(x)的值域;
時,求函數f(x)的值域;
(2)若![]() 且sinB+sinC=
且sinB+sinC=![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com