
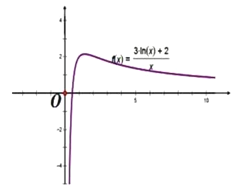
【題目】(1)已知函數![]() ,求函數
,求函數![]() 在
在![]() 時的值域;
時的值域;
(2)函數![]() 有兩個不同的極值點
有兩個不同的極值點![]() ,
,![]() ,
,
①求實數![]() 的取值范圍;
的取值范圍;
②證明:![]() .
.
(本題中可以參與的不等式:![]() ,
,![]() )
)
【答案】(1)![]() (2)①
(2)①![]() ②詳見解析
②詳見解析
【解析】
(1)首先可對函數![]() 進行求導,然后分析函數
進行求導,然后分析函數![]() 在
在![]() 上的單調性并求出最值,最后即可求出函數
上的單調性并求出最值,最后即可求出函數![]() 在
在![]() 上的值域;
上的值域;
(2)①首先將“![]() 有兩個不同極值點”轉化為“
有兩個不同極值點”轉化為“![]() 有兩個不同的正實根”,再根據(1)中所給出的函數性質即可得出結果;
有兩個不同的正實根”,再根據(1)中所給出的函數性質即可得出結果;
②可利用分析法進行證明。
(1)![]() ,令
,令![]() ,
,![]() ,
,
![]() 在
在![]() 上有
上有![]() ,
,![]() 在
在![]() 上有
上有![]() ,
,
從而有![]() 在
在![]() 上為單增函數,在
上為單增函數,在![]() 上為單減函數,
上為單減函數,
![]() ,且當
,且當![]() 時,
時,![]() ,故函數
,故函數![]() 的值域為
的值域為![]() ;
;
(2)①![]() ,
,
題意![]() 有兩個不同極值點即
有兩個不同極值點即![]() 有兩個不同的正實數根,即
有兩個不同的正實數根,即![]() 有兩個不同的正實根,
有兩個不同的正實根,
由(1)題函數![]() 的性質知:
的性質知:![]() ,故
,故![]() ;
;
②由條件![]() 有兩個不同的極值點
有兩個不同的極值點![]() ,
,![]() 知:
知:
![]() ,于是有
,于是有![]()
所以![]() ,即
,即![]()
要證![]() 成立,只需證明
成立,只需證明![]()
只需證![]()
只需證![]()
只需證![]()
只需證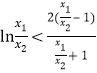 ,令
,令![]() ,
,![]()
只需證![]() ,
,![]() ,而題中已給出該不等式成立.
,而題中已給出該不等式成立.
即證![]() 。
。


 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,已知直線
中,已知直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,以
為參數),以坐標原點為極點,以![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點.
兩點.
(1)求直線![]() l的普通方程和曲線
l的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點![]() 的極坐標為
的極坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,直線
,直線![]() 為平面內的動點,過點
為平面內的動點,過點![]() 作直線
作直線![]() 的垂線,垂足為點
的垂線,垂足為點![]() ,且
,且![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過點![]() 作兩條互相垂直的直線
作兩條互相垂直的直線![]() 與
與![]() 分別交軌跡
分別交軌跡![]() 于
于![]() 四點.求
四點.求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在極坐標系中,O為極點,點![]() 在曲線
在曲線![]() 上,直線l過點
上,直線l過點![]() 且與
且與![]() 垂直,垂足為P.
垂直,垂足為P.
(1)當![]() 時,求
時,求![]() 及l的極坐標方程;
及l的極坐標方程;
(2)當M在C上運動且P在線段OM上時,求P點軌跡的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】動圓P過點![]() ,且與直線
,且與直線![]() 相切,設動圓圓心
相切,設動圓圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)過點F的直線交曲線C于A,B兩個不同的點,過點A,B分別作曲線C的切線,且二者相交于點M,若直線![]() 的斜率為
的斜率為![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,共享單車已經悄然進入了廣大市民的日常生活,并慢慢改變了人們的出行方式.為了更好地服務民眾,某共享單車公司在其官方![]() 中設置了用戶評價反饋系統,以了解用戶對車輛狀況和優惠活動的評價.現從評價系統中選出
中設置了用戶評價反饋系統,以了解用戶對車輛狀況和優惠活動的評價.現從評價系統中選出![]() 條較為詳細的評價信息進行統計,車輛狀況的優惠活動評價的
條較為詳細的評價信息進行統計,車輛狀況的優惠活動評價的![]() 列聯表如下:
列聯表如下:
對優惠活動好評 | 對優惠活動不滿意 | 合計 | |
對車輛狀況好評 |
|
|
|
對車輛狀況不滿意 |
|
|
|
合計 |
|
|
|
(1)能否在犯錯誤的概率不超過![]() 的前提下認為優惠活動好評與車輛狀況好評之間有關系?
的前提下認為優惠活動好評與車輛狀況好評之間有關系?
(2)為了回饋用戶,公司通過![]() 向用戶隨機派送每張面額為
向用戶隨機派送每張面額為![]() 元,
元,![]() 元,
元,![]() 元的 三種騎行券.用戶每次使用
元的 三種騎行券.用戶每次使用![]() 掃碼用車后,都可獲得一張騎行券.用戶騎行一次獲得
掃碼用車后,都可獲得一張騎行券.用戶騎行一次獲得![]() 元券,獲得
元券,獲得![]() 元券的概率分別是
元券的概率分別是![]() ,
,![]() ,且各次獲取騎行券的結果相互獨立.若某用戶一天使用了兩次該公司的共享單車,記該用戶當天獲得的騎行券面額之和為
,且各次獲取騎行券的結果相互獨立.若某用戶一天使用了兩次該公司的共享單車,記該用戶當天獲得的騎行券面額之和為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班上午有五節課,分別安排語文,數學,英語,物理,化學各一節課.要求語文與化學相鄰,數學與物理不相鄰,且數學課不排第一節,則不同排課法的種數是
A. 24B. 16C. 8D. 12
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年10月,德國爆發出“芳香烴門”事件,即一家權威的檢測機構在德國銷售的奶粉中隨機抽檢了16款(德國4款,法國8款,荷蘭4款),其中8款檢測出芳香烴礦物油成分,此成分會嚴重危害嬰幼兒的成長,有些奶粉已經遠銷至中國.A地區聞訊后,立即組織相關檢測員對這8款品牌的奶粉進行抽檢,已知該地區有6家嬰幼兒用品商店在售這幾種品牌的奶粉,甲、乙、丙3名檢測員分別負責進行檢測,每人至少抽檢1家商店,且檢測過的商店不重復檢測,則甲檢測員檢測2家商店的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知直線![]() 與曲線
與曲線![]() 相切于兩點,則對于函數
相切于兩點,則對于函數![]() ,以下結論成立的是( )
,以下結論成立的是( )

A.有3個極大值點,2個極小值點B.有2個零點
C.有2個極大值點,沒有極小值點D.沒有零點
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com