
某電視臺組織部分記者,用“10分制”隨機調查某社區居民的幸福指數.現從調查人群中隨機抽取16名,如圖所示的莖葉圖記錄了他們的幸福指數的得分(以小數點前的一位數字為莖,小數點后的一位數字為葉):
(1)指出這組數據的眾數和中位數;
(2)若幸福指數不低于9.5分,則稱該人的幸福指數為“極幸福”.求從這16人中隨機選取3人,至多有1人是“極幸福”的概率;
(3)以這16人的樣本數據來估計整個社區的總體數據,若從該社區(人數很多)任選3人,記 表示抽到“極幸福”的人數,求
表示抽到“極幸福”的人數,求 的分布列及數學期望.
的分布列及數學期望.
(1)8.6,8.75;(2)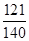 ;(3)參考解析
;(3)參考解析
解析試題分析:(1)由眾數即為樣本中出現次數最多的數字,中位數即為樣本數據從小到大排序最中間的那個數字或是最中間的兩個數字.根據所給的數字即可得到結論.
科目:高中數學
來源:
題型:解答題
某校100名學生期中考試語文成績的頻率分布直方圖如圖所示,其中成績分組區間是:[50,60][60,70][70,80][80,90][90,100].
科目:高中數學
來源:
題型:解答題
某企業有兩個分廠生產某種零件,按規定內徑尺寸(單位:mm)的值落在[29.94,30.06)的零件為優質品.從兩個分廠生產的零件中各抽出了500件,量其內徑尺寸,得結果如下表:
科目:高中數學
來源:
題型:解答題
大家知道,莫言是中國首位獲得諾貝爾獎的文學家,國人歡欣鼓舞.某高校文學社從男女生中各抽取50名同學調查對莫言作品的了解程度,結果如下:
科目:高中數學
來源:
題型:解答題
某地區有小學21所,中學14所,大學7所,現采用分層抽樣的方法從這些學校中抽取6所學校對學生進行視力調查.
科目:高中數學
來源:
題型:解答題
某批次的某種燈泡共
科目:高中數學
來源:
題型:解答題
某工廠有25周歲以上(含25周歲)工人300名,25周歲以下工人200名.為研究工人的日平均生產量是否與年齡有關.現采用分層抽樣的方法,從中抽取了100名工人,先統計了他們某月的日平均生產件數,然后按工人年齡在“25周歲以上(含25周歲)”和“25周歲以下”分為兩組,在將兩組工人的日平均生產件數分成5組:
科目:高中數學
來源:
題型:解答題
甲、乙兩位學生參加數學競賽培訓,在培訓期間,他們參加的
科目:高中數學
來源:
題型:解答題
在某次數學考試中,抽查了1000名學生的成績,得到頻率分布直方圖如圖所示,規定85分及其以上為優秀.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
(2)因為幸福指數不低于9.5分的共有4人,求從這16人中隨機選取3人,至多有1人是“極幸福”的概率,轉化為16人中一人是“極幸福”的概率加上沒有人是“極幸福”的概率.通過計算即可得到所求的結論.
(3)若從該社區(人數很多)任選3人,記 表示抽到“極幸福”的人數,共有四種情況,并且分別求出各種情況的概率,從而得到數學期望值.
表示抽到“極幸福”的人數,共有四種情況,并且分別求出各種情況的概率,從而得到數學期望值.
試題解析:(1)眾數:8.6;中位數:8.75 ;
(2)設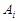 表示所取3人中有
表示所取3人中有 個人是“極幸福”,至多有1人是“極幸福”記為事件
個人是“極幸福”,至多有1人是“極幸福”記為事件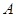 , 則
, 則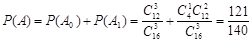 ;
;
(3)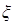 的可能取值為0,1,2,3.
的可能取值為0,1,2,3.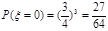 ;
;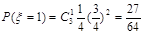 ;
;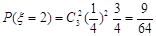 ;
;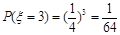 .
.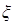 的分布列為:
的分布列為: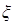

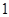
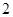


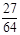
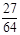
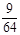
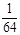
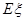
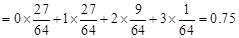 .
.
另解: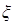 的可能取值為0,1,2,3,則
的可能取值為0,1,2,3,則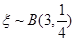 ,因此
,因此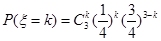 .
.
有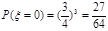 ;
;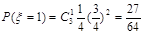 ;
;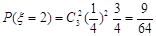 ;
;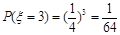 .
.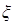 的分布列為:
的分布列為: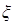




課課練與單元測試系列答案
世紀金榜小博士單元期末一卷通系列答案
單元測試AB卷臺海出版社系列答案
黃岡新思維培優考王單元加期末卷系列答案
名校名師奪冠金卷系列答案
小學英語課時練系列答案
培優新幫手系列答案


課堂作業廣西教育出版社系列答案
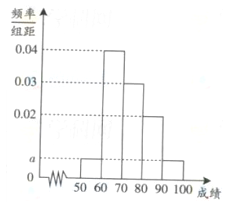
(1)求圖中a的值;
(2)根據頻率分布直方圖,估計這100名學生語文成績的平均分;
(3)若這100名學生語文成績某些分數段的人數(x)與數學成績相應分數段的人數(y)之比如下表所示,求數學成績在[50,90)之外的人數.
甲廠:
乙廠:分組
[29.86,29.90)
[29.90,29.94)
[29.94,29.98)
[29.9830.02),
[30.02,30.06)
[30.06,30.10)
[30.10,30.14)
頻數
12
63
86
182
92
61
4
分組
[29.86,29.90)
[29.90,29.94)
[29.94,29.98)
[29.9830.02),
[30.02,30.06)
[30.06,30.10)
[30.10,30.14)
頻數
29
71
85
159
76
62
18
(1)試分別估計兩個分廠生產的零件的優質品率;
(2)由以上統計數據填下面2×2列聯表,并問是否有99%的把握認為“兩個分廠生產的零件的質量有差異”?
附:
甲廠
乙廠
合計
優質品
非優質品
合 計
P(χ2≥x0)
0.05
0.01
x0
3.841
6.635
(1)試估計該校學生閱讀莫言作品超過50篇的概率;閱讀過莫言的
作品數(篇)
0~25
26~50
51~75
76~100
101~130
男生
3
6
11
18
12
女生
4
8
13
15
10
(2)對莫言作品閱讀超過75篇的則稱為“對莫言作品非常了解”,否則為“一般了解”.根據題意完成下表,并判斷能否有75%的把握認為對莫言作品的非常了解與性別有關?
附:
非常了解
一般了解
合計
男生
女生
合計
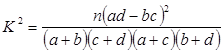
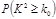
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
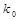
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
(1)求應從小學、中學、大學中分別抽取的學校數目;
(2)若從抽取的6所學校中隨機抽取2所學校做進一步數據分析,
①列出所有可能的抽取結果;
②求抽取的2所學校均為小學的概率. 個,對其壽命進行追蹤調查,將結果列成頻率分布表如下.根據壽命將燈泡分成優等品、正品和次品三個等級,其中壽命大于或等于
個,對其壽命進行追蹤調查,將結果列成頻率分布表如下.根據壽命將燈泡分成優等品、正品和次品三個等級,其中壽命大于或等于 天的燈泡是優等品,壽命小于
天的燈泡是優等品,壽命小于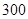 天的燈泡是次品,其余的燈泡是正品.
天的燈泡是次品,其余的燈泡是正品.
(1)根據頻率分布表中的數據,寫出壽命(天) 頻數 頻率 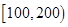


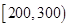


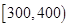


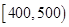
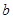
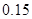
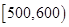

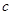
合計 

 、
、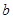 、
、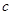 的值;
的值;
(2)某人從這 個燈泡中隨機地購買了
個燈泡中隨機地購買了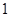 個,求此燈泡恰好不是次品的概率;
個,求此燈泡恰好不是次品的概率;
(3)某人從這批燈泡中隨機地購買了 個,如果這
個,如果這 個燈泡的等級情況恰好與按三個等級分層抽樣所得的結果相同,求
個燈泡的等級情況恰好與按三個等級分層抽樣所得的結果相同,求 的最小值.
的最小值.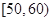 ,
,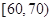 ,
, ,
,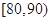 ,
,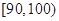 分別加以統計,得到如圖所示的頻率分布直方圖.
分別加以統計,得到如圖所示的頻率分布直方圖.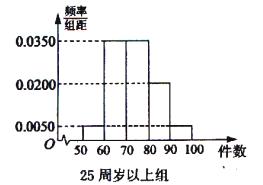
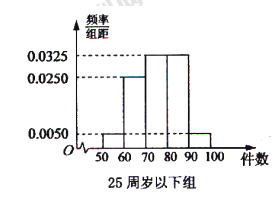

(1)從樣本中日平均生產件數不足60件的工人中隨機抽取2人,求至少抽到一名“25周歲以下組”工人的頻率.
(2)規定日平均生產件數不少于80件者為“生產能手”,請你根據已知條件完成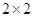 的列聯表,并判斷是否有
的列聯表,并判斷是否有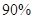 的把握認為“生產能手與工人所在的年齡組有關”?
的把握認為“生產能手與工人所在的年齡組有關”?
附表: 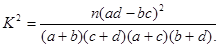
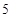 次預賽成績記錄如下:
次預賽成績記錄如下:
甲 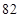
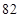

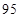
 乙
乙 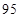


(1)用莖葉圖表示這兩組數據;
(2)從甲、乙兩人的成績中各隨機抽取一個,求甲的成績比乙高的概率;
(3)①求甲、乙兩人的成績的平均數與方差,②若現要從中選派一人參加數學競賽,
根據你的計算結果,你認為選派哪位學生參加合適?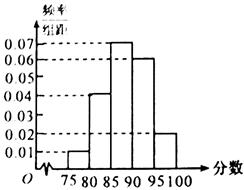
(1)下表是這次抽查成績的頻數分布表,試求正整數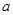 、
、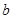 的值;
的值;
(2)現在要用分層抽樣的方法從這1000人中抽取40人的成績進行分析,求抽取成績為優秀的學生人數;區間
[75,80)
[80,85)
[85,90)
[90,95)
[95,100]
人數
50
a
350
300
b
(3)在根據(2)抽取的40名學生中,要隨機選取2名學生參加座談會,記其中成績為優秀的人數為X,求X的分布列與數學期望(即均值).
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號