
【題目】已知函數![]() .
.
(Ⅰ)當![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(Ⅱ)求函數![]() 的單調區間;
的單調區間;
(Ⅲ)若對任意的![]() ,都有
,都有![]() 成立,求a的取值范圍.
成立,求a的取值范圍.
【答案】(Ⅰ)![]() (Ⅱ)當
(Ⅱ)當![]() 時增區間為
時增區間為![]() 當
當![]() 時增區間為
時增區間為![]() ,減區間為
,減區間為![]() (Ⅲ)
(Ⅲ)![]()
【解析】
試題(Ⅰ)利用導數的幾何意義得到切線的斜率,進而得到切線方程(Ⅱ)首先計算函數的導數,令導數大于零可得增區間,進而得到減區間,求解時注意對參數的取值范圍分情況討論(Ⅲ)不等式恒成立問題中求參數范圍的一般采用分離參數的方法,轉化為求函數的最值問題
試題解析:(Ⅰ)![]() 時,
時,![]()
![]()
曲線![]() 在點
在點![]() 處的切線方程
處的切線方程![]()
(Ⅱ)![]()
①當![]() 時,
時,![]() 恒成立,函數
恒成立,函數![]() 的遞增區間為
的遞增區間為![]()
②當![]() 時,令
時,令![]() ,解得
,解得![]() 或
或![]()
x | ( 0, |
| ( |
f’(x) | - | + | |
f(x) | 減 | 增 |
所以函數![]() 的遞增區間為
的遞增區間為![]() ,遞減區間為
,遞減區間為![]()
(Ⅲ)對任意的![]() ,使
,使![]() 成立,只需任意的
成立,只需任意的![]() ,
,![]()
①當![]() 時,
時,![]() 在
在![]() 上是增函數,
上是增函數,
所以只需![]()
而![]()
所以![]() 滿足題意;
滿足題意;
②當![]() 時,
時,![]() ,
,![]() 在
在![]() 上是增函數,
上是增函數,
所以只需![]()
而![]()
所以![]() 滿足題意;
滿足題意;
③當![]() 時,
時,![]() ,
,![]() 在
在![]() 上是減函數,
上是減函數,![]() 上是增函數,
上是增函數,
所以只需![]() 即可
即可
而![]()
從而![]() 不滿足題意;
不滿足題意;
綜合①②③實數![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓E:![]() 的焦點在
的焦點在![]() 軸上,A是E的左頂點,斜率為k (k > 0)的直線交E于A,M兩點,點N在E上,MA⊥NA.
軸上,A是E的左頂點,斜率為k (k > 0)的直線交E于A,M兩點,點N在E上,MA⊥NA.
(Ⅰ)當t=4,![]() 時,求△AMN的面積;
時,求△AMN的面積;
(Ⅱ)當![]() 時,求k的取值范圍.
時,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列有關命題的說法正確的是( )
A. ![]() ,使得
,使得![]() 成立.
成立.
B. 命題![]() :任意
:任意![]() ,都有
,都有![]() ,則
,則![]() :存在
:存在![]() ,使得
,使得![]() .
.
C. 命題“若![]() 且
且![]() ,則
,則![]() 且
且![]() ”的逆命題為真命題.
”的逆命題為真命題.
D. 若數列![]() 是等比數列,
是等比數列,![]() 則
則![]() 是
是![]() 的必要不充分條件.
的必要不充分條件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,
,![]() 的兩頂點
的兩頂點![]() ,且點
,且點![]() 滿足
滿足![]()
(1)求動點![]() 的軌跡方程;
的軌跡方程;![]()
(2)設![]() ,求動點
,求動點![]() 的軌跡方程;
的軌跡方程;
(3)過點![]() 的動直線
的動直線![]() 與曲線
與曲線![]() 交于不同兩點
交于不同兩點![]() ,過點
,過點![]() 作
作![]() 軸垂線
軸垂線![]() ,試判斷直線
,試判斷直線![]() 與直線
與直線![]() 的交點是否恒在一條定直線上?若是,求該定直線的方程,否則,說明理由.
的交點是否恒在一條定直線上?若是,求該定直線的方程,否則,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某老師是省級課題組的成員,主要研究課堂教學目標達成度,為方便研究,從實驗班中隨機抽取30次的隨堂測試成績進行數據分析.已知學生甲的30次隨堂測試成績如下(滿分為100分):
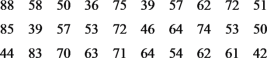
(1)把學生甲的成績按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6組,列出頻率分布表,并畫出頻率分布直方圖:
分成6組,列出頻率分布表,并畫出頻率分布直方圖:
(2)為更好的分析學生甲存在的問題,從隨堂測試成績50分以下(不包括50分)的試卷中隨機抽取3份進行分析,求恰有2份成績在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某醫院用光電比色計檢查尿汞時,得尿汞含量(毫克/升)與消光系數如下表:
尿汞含量 | 2 | 4 | 6 | 8 | 10 |
消光系數 | 64 | 138 | 205 | 285 | 360 |
(1)作散點圖;
(2)如果![]() 與
與![]() 之間具有線性相關關系,求回歸線直線方程;
之間具有線性相關關系,求回歸線直線方程;
(3)估計尿汞含量為9毫克/升時消光系數.
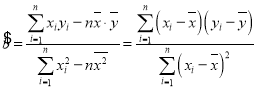 ,
,![]() .
.
參考數據:![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com