
【題目】已知橢圓E:![]() 的焦點在
的焦點在![]() 軸上,A是E的左頂點,斜率為k (k > 0)的直線交E于A,M兩點,點N在E上,MA⊥NA.
軸上,A是E的左頂點,斜率為k (k > 0)的直線交E于A,M兩點,點N在E上,MA⊥NA.
(Ⅰ)當t=4,![]() 時,求△AMN的面積;
時,求△AMN的面積;
(Ⅱ)當![]() 時,求k的取值范圍.
時,求k的取值范圍.
 智趣寒假作業云南科技出版社系列答案
智趣寒假作業云南科技出版社系列答案科目:高中數學 來源: 題型:
【題目】某地區高考實行新方案,規定:語文、數學和英語是考生的必考科目,考生還須從物理、化學、生物、歷史、地理和政治六個科目中選取三個科目作為選考科目,若一名學生從六個科目中選出了三個科目作為選考科目,則稱該學生的選考方案確定;否則,稱該學生選考方案待確定.例如,學生甲選擇“物理、化學和生物”三個選考科目,則學生甲的選考方案確定,“物理、化學和生物”為其選考方案.
某學校為了了解高一年級420名學生選考科目的意向,隨機選取30名學生進行了一次調查,統計選考科目人數如下表:
性別 | 選考方案確定情況 | 物理 | 化學 | 生物 | 歷史 | 地理 | 政治 |
男生 | 選考方案確定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
選考方案待確定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 選考方案確定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
選考方案待確定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(Ⅰ)估計該學校高一年級選考方案確定的學生中選考生物的學生有多少人?
(Ⅱ)假設男生、女生選擇選考科目是相互獨立的.從選考方案確定的8位男生隨機選出1人,從選考方案確定的10位女生中隨機選出1人,試求該男生和該女生的選考方案中都含有歷史科目的概率;
(Ⅲ)從選考方案確定的8名男生隨機選出2名,設隨機變量兩名男生選考方案相同時![]() ,兩名男生選考方案不同時
,兩名男生選考方案不同時![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,已知圓![]() 的方程為
的方程為![]() ,圓
,圓![]() 的方程為
的方程為![]() ,動圓
,動圓![]() 與圓
與圓![]() 內切且與圓
內切且與圓![]() 外切.
外切.
(1)求動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)已知![]() 與
與![]() 為平面內的兩個定點,過
為平面內的兩個定點,過![]() 點的直線
點的直線![]() 與軌跡
與軌跡![]() 交于
交于![]() ,
,![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】進入12月以來,某地區為了防止出現重污染天氣,堅持保民生、保藍天,嚴格落實機動車限行等一系列“管控令”.該地區交通管理部門為了了解市民對“單雙號限行”的贊同情況,隨機采訪了220名市民,將他們的意見和是否擁有私家車情況進行了統計,得到如下的![]() 列聯表:
列聯表:
贊同限行 | 不贊同限行 | 合計 | |
沒有私家車 | 90 | 20 | 110 |
有私家車 | 70 | 40 | 110 |
合計 | 160 | 60 | 220 |
(1)根據上面的列聯表判斷,能否在犯錯誤的概率不超過0.001的前提下認為“是否贊同限行與是否擁有私家車”有關;
(2)為了了解限行之后是否對交通擁堵、環境污染起到改善作用,從上述調查的不贊同限行的人員中按分層抽樣抽取6人,再從這6人中隨機抽出3名進行電話回訪,求3人中至少抽到1名“沒有私家車”人員的概率.
附:![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高三理科班共有60名同學參加某次考試,從中隨機挑選出5名同學,他們的數學成績![]() 與物理成績
與物理成績![]() 如下表:
如下表:

數據表明![]() 與
與![]() 之間有較強的線性關系.
之間有較強的線性關系.
(1)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)該班一名同學的數學成績為110分,利用(1)中的回歸方程,估計該同學的物理成績;
(3)本次考試中,規定數學成績達到125分為優秀,物理成績達到100分為優秀.若該班數學優秀率與物理優秀率分別為![]() 和
和![]() ,且除去抽走的5名同學外,剩下的同學中數學優秀但物理不優秀的同學共有5人.能否在犯錯誤概率不超過0.01的前提下認為數學優秀與物理優秀有關?
,且除去抽走的5名同學外,剩下的同學中數學優秀但物理不優秀的同學共有5人.能否在犯錯誤概率不超過0.01的前提下認為數學優秀與物理優秀有關?
參考數據:回歸直線的系數 ,
,![]() .
.
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用適當的方法表示下列集合:
(1)一年中有31天的月份的全體;
(2)大于![]() 小于12.8的整數的全體;
小于12.8的整數的全體;
(3)梯形的全體構成的集合;
(4)所有能被3整除的數的集合;
(5)方程![]() 的解組成的集合;
的解組成的集合;
(6)不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大連市某企業為確定下一年投入某種產品的宣傳費,需了解年宣傳費![]() (單位:千元)對年銷售量
(單位:千元)對年銷售量![]() (單位:
(單位:![]() )和年利潤
)和年利潤![]() (單位:千元)的影響,對近8年的年宣傳費
(單位:千元)的影響,對近8年的年宣傳費![]() 和年銷售量
和年銷售量![]() 數據作了初步處理,得到下面的散點圖及一些統計量的值.
數據作了初步處理,得到下面的散點圖及一些統計量的值.

|
|
|
|
|
|
|
46.6 | 573 | 6.8 | 289.8 | 1.6 | 215083.4 | 31280 |
表中![]() ,
,![]() .
.
根據散點圖判斷,
![]() 與
與![]() 哪一個適宜作為年銷售量
哪一個適宜作為年銷售量![]() 關于年宣傳費
關于年宣傳費![]() 的回歸方程類型?(給出判斷即可,不必說明理由)
的回歸方程類型?(給出判斷即可,不必說明理由)
![]() 根據
根據![]() 的判斷結果及表中數據,建立
的判斷結果及表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
![]() 已知這種產品的年利潤
已知這種產品的年利潤![]() 與
與![]() 、
、![]() 的關系為
的關系為![]() .根據
.根據![]() 的結果回答下列問題:
的結果回答下列問題:
![]() 年宣傳費
年宣傳費![]() 時,年銷售量及年利潤的預報值是多少?
時,年銷售量及年利潤的預報值是多少?
![]() 年宣傳費
年宣傳費![]() 為何值時,年利潤的預報值最大?
為何值時,年利潤的預報值最大?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為:
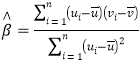 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的一個焦點與拋物線
的一個焦點與拋物線![]() 的焦點
的焦點![]() 重合,且橢圓短軸的兩個端點與點
重合,且橢圓短軸的兩個端點與點![]() 構成正三角形.
構成正三角形.
(1)求橢圓的方程;
(2)若過點![]() 的直線
的直線![]() 與橢圓交于不同的兩點
與橢圓交于不同的兩點![]() ,試問在
,試問在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使
,使![]() 恒為定值?若存在,求出
恒為定值?若存在,求出![]() 的坐標,并求出這個定值;若不存在,請說明理由.
的坐標,并求出這個定值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com