
 如圖所示,正三角形ABC的外接圓半徑為2,圓心為O,PB=PC=2,D為AP上一點,AD=2DP,點D在平面ABC內的射影為圓心O.
如圖所示,正三角形ABC的外接圓半徑為2,圓心為O,PB=PC=2,D為AP上一點,AD=2DP,點D在平面ABC內的射影為圓心O.分析 (Ⅰ)連結AOL,并延長交BC于點E,連結PE,推導出DO∥PE,由此能證明DO∥平面PBC.
(Ⅱ)以點E為坐標原點,以EO、EB、EP所在直線分別為x軸、y軸、z軸,建立空間直角坐標系,利用向量法能求出平面CBD和平面OBD所成銳二面角的余弦值.
解答 證明:(Ⅰ)連結AO,并延長交BC于點E,連結PE,
∵O為正三角形ABC的外接圓圓心,
∴AO=2OE,
又AD=2DP,∴DO∥PE,
∵PE?平面PBC,DO?平面PBC,
∴DO∥平面PBC.
解:(Ⅱ)由(Ⅰ)知,DO⊥平面ABC,
∵DO∥PE,∴PE⊥平面ABC,
∴PE⊥BC,PE⊥AE,又AE⊥BC,
∴以點E為坐標原點,以EO、EB、EP所在直線分別為x軸、y軸、z軸,
建立空間直角坐標系,
則E(0,0,0),O(1,0,0),B(0,$\sqrt{3}$,0),P(0,0,1),A(3,0,0),
∴$\overrightarrow{EB}$=(0,$\sqrt{3}$,0),$\overrightarrow{AP}$=(-3,0,1),$\overrightarrow{AD}$=(-2,0,$\frac{2}{3}$),$\overrightarrow{ED}$=$\overrightarrow{EA}+\overrightarrow{AD}$=(1,0,$\frac{2}{3}$),
∴D(1,0,$\frac{2}{3}$),$\overrightarrow{OD}$=(0,0,$\frac{2}{3}$),$\overrightarrow{BO}$=(1,-$\sqrt{3}$,0),
設平面CDB的一個法向量$\overrightarrow{n}$=(x,y,z),
則$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EB}=\sqrt{3}y=0}\\{\overrightarrow{n}•\overrightarrow{ED}=x+\frac{2}{3}z=0}\end{array}\right.$,取z=1,得$\overrightarrow{n}$=(-$\frac{2}{3}$,0,1),
設平面BOD的法向量為$\overrightarrow{m}$=(a,b,c),
則$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BO}=a-\sqrt{3}b=0}\\{\overrightarrow{m}•\overrightarrow{OD}=\frac{2}{3}c=0}\end{array}\right.$,取a=1,得$\overrightarrow{m}$=(1,$\frac{\sqrt{3}}{3}$,0),
cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{-\frac{2}{3}}{\sqrt{\frac{4}{9}+1}•\sqrt{1+\frac{1}{3}}}$=-$\frac{\sqrt{39}}{13}$,
∴平面CBD和平面OBD所成銳二面角的余弦值為$\frac{\sqrt{39}}{13}$.
點評 本題考查線面平行的證明,考查二面角的余弦值的求法,是中檔題,解題時要認真審題,注意向量法的合理運用.


 名校通行證有效作業系列答案
名校通行證有效作業系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
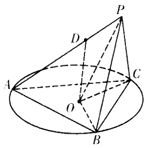 如圖所示,正三角形ABC的外接圓半徑為2,圓心為O,PB=PC=2,D為AP上一點,AD=2DP,點D在平面ABC內的射影為圓心O.
如圖所示,正三角形ABC的外接圓半徑為2,圓心為O,PB=PC=2,D為AP上一點,AD=2DP,點D在平面ABC內的射影為圓心O.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com