
【題目】設![]() 是定義在
是定義在![]() 上的奇函數,且對任意實數
上的奇函數,且對任意實數![]() ,恒有
,恒有![]() ,當
,當![]() 時,
時, ![]()
(1)求證: ![]() 是周期函數;
是周期函數;
(2)當![]() 時,求
時,求![]() 的解析式;
的解析式;
(3)計算![]()
【答案】(1)證明見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】試題分析:(1)根據條件利用![]() 是定義在
是定義在![]() 上的奇函數,
上的奇函數, ![]() ,可得
,可得![]() ,從而證得結論;(2)利用函數的奇偶性和周期性,求得當
,從而證得結論;(2)利用函數的奇偶性和周期性,求得當![]() 時,函數
時,函數![]() 的解析式;(3)利用周期為
的解析式;(3)利用周期為![]() 以及
以及![]() 的值,可得
的值,可得![]() 的值.
的值.
試題解析:(1)證明:∵![]() ,∴
,∴![]() .∴
.∴![]() 是周期為4的周期函數.
是周期為4的周期函數.
(2)∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,即
,即![]()
(3)∵![]()
又![]() 是周期為4的周期函數,
是周期為4的周期函數,
![]()
![]()
【方法點晴】本題主要考查函數的解析式及函數的周期性,屬于難題.對函數周期性的考查主要命題方向由兩個,一是三角函數,可以用公式求出周期;二是抽象函數,往往需要根據條件判斷出周期,抽象函數給出條件判斷周期的常見形式為:
(1) ![]() ;(2)
;(2)![]() ;
;
(3) ![]() .
.


科目:高中數學 來源: 題型:
【題目】已知p:x∈R,cos2x﹣sinx+2≤m;q:函數 ![]() 在[1,+∞)上單調遞減.
在[1,+∞)上單調遞減.
(I)若p∧q為真命題,求m的取值范圍;
(II)若p∨q為真命題,p∧q為假命題,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足(an+1﹣1)(an﹣1)=3(an﹣an+1),a1=2,令 ![]() .
.
(Ⅰ)證明:數列{bn}是等差數列;
(Ⅱ)求數列{an}的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC=90°,AB= ![]() ,BC=1,P為△ABC內一點,∠BPC=90°.
,BC=1,P為△ABC內一點,∠BPC=90°. 
(1)若PB= ![]() ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個化肥廠生產甲、乙兩種混合肥料,生產1車皮甲種肥料的主要原料是磷酸鹽4t,硝酸鹽18t;生產1車乙種肥料的主要原料是磷酸鹽1t、硝酸鹽15t.現庫存磷酸鹽10t、硝酸鹽66t.已知生產1車皮甲種肥料,產生的利潤為10000元;生產1車皮乙種肥料,產生的利潤為5000元.那么分別生產甲、乙兩種肥料各多少車皮,能夠產生最大利潤?最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“微信運動”已成為當下熱門的健身方式,小王的微信朋友圈內也有大量好友參與了“微信運動”,他隨機選取了其中的40人(男、女各20人),記錄了他們某一天的走路步數,并將數據整理如下:
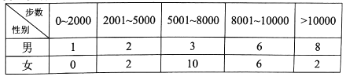
(1)若采用樣本估計總體的方式,試估計小王的所有微信好友中每日走路步數超過5000步的概率;
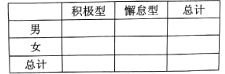
(2)已知某人一天的走路步數超過8000步被系統評定“積極型”,否則為“懈怠型”,根據題意完成下面的![]() 列聯表,并據此判斷能否有95%以上的把握認為“評定類型”與“性別”有關?
列聯表,并據此判斷能否有95%以上的把握認為“評定類型”與“性別”有關?
附: 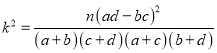 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com