
【題目】已知點A(1, ![]() )在橢圓E:
)在橢圓E: ![]() =1上,若斜率為
=1上,若斜率為 ![]() 的直線l與橢圓E交于B,C兩點,當△ABC的面積最大時,求直線l的方程.
的直線l與橢圓E交于B,C兩點,當△ABC的面積最大時,求直線l的方程.
【答案】解:設直線l的方程為y= ![]() x+m,設B(x1 , y1),C(x2 , y2),
x+m,設B(x1 , y1),C(x2 , y2),
由 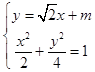 ,消去y,整理得4x2+2
,消去y,整理得4x2+2 ![]() mx+m2﹣4=0,
mx+m2﹣4=0,
則△=8m2﹣16(m2﹣4)=8(8﹣m2)>0,解得:0≤m2<8,
由韋達定理可知:x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
由弦長公式可知:丨BC丨= ![]()
![]() =
= ![]() ,
,
又點A到l的距離為d= 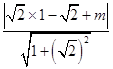 =
= ![]() ,
,
故S△ABC= ![]() 丨BC丨d=
丨BC丨d= 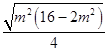 =
= ![]()
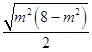 ≤
≤ ![]()
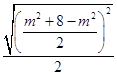 =
= ![]() ,
,
當且僅當 m2=8﹣m2 , 即m=±2時取等號,此時滿足0≤m2<8,
故直線l的方程為y= ![]() x±2.
x±2.
【解析】由題意可知:設直線l的方程為y= ![]() x+m,代入橢圓方程,由△>0,求得0≤m2<8,根據韋達定理及弦長公式求得丨BC丨,由點到直線的距離公式點A到l的距離為d,再利用三角形的面積公式求得S△ABC=
x+m,代入橢圓方程,由△>0,求得0≤m2<8,根據韋達定理及弦長公式求得丨BC丨,由點到直線的距離公式點A到l的距離為d,再利用三角形的面積公式求得S△ABC= ![]() 丨BC丨d,利用基本不等式的性質即可求得△ABC的面積最大值時,m的取值,即可求得直線l的方程.
丨BC丨d,利用基本不等式的性質即可求得△ABC的面積最大值時,m的取值,即可求得直線l的方程.


科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以原點為極點,
中,以原點為極點, ![]() 軸的非負半軸為極軸建立極坐標系,已知直線
軸的非負半軸為極軸建立極坐標系,已知直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),曲線
為參數),曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某建材公司在![]() ,
,![]() 兩地各有一家工廠,它們生產的建材由公司直接運往
兩地各有一家工廠,它們生產的建材由公司直接運往![]() 地.由于土路交通運輸不便,為了減少運費,該公司預備投資修建一條從
地.由于土路交通運輸不便,為了減少運費,該公司預備投資修建一條從![]() 地或
地或![]() 地直達
地直達![]() 地的公路;若選擇從某地修建公路,則另外一地生產的建材可先運輸至該地再運至
地的公路;若選擇從某地修建公路,則另外一地生產的建材可先運輸至該地再運至![]() 以節約費用.已知
以節約費用.已知![]() ,
,![]() 之間為土路,土路運費為每噸千米20元,公路的運費減半,
之間為土路,土路運費為每噸千米20元,公路的運費減半,![]() ,
,![]() ,
,![]() 三地距離如圖所示.為了制定修路計劃,公司統計了最近10天兩個工廠每天的建材產量,得到下面的柱形圖,以兩個工廠在最近10天日產量的頻率代替日產量的概率.
三地距離如圖所示.為了制定修路計劃,公司統計了最近10天兩個工廠每天的建材產量,得到下面的柱形圖,以兩個工廠在最近10天日產量的頻率代替日產量的概率.
(1)求“![]() ,
,![]() 兩地工廠某天的總日產量為20噸”的概率;
兩地工廠某天的總日產量為20噸”的概率;
(2)以修路后每天總的運費的期望為依據,判斷從![]() ,
,![]() 哪一地修路更加劃算.
哪一地修路更加劃算.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了檢測某種產品的質量(單位:千克),抽取了一個容量為N的樣本,整理得到的數據作出了頻率分布表和頻率分布直方圖如圖:
分組 | 頻數 | 頻率 |
[17.5,20) | 10 | 0.05 |
[20,225) | 50 | 0.25 |
[22.5,25) | a | b |
[25,27.5) | 40 | c |
[27.5,30] | 20 | 0.10 |
合計 | N | 1 |
(Ⅰ)求出表中N及a,b,c的值;
(Ⅱ)求頻率分布直方圖中d的值;
(Ⅲ)從該產品中隨機抽取一件,試估計這件產品的質量少于25千克的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】O為原點的直角坐標系中,點A(4,﹣3)為△OAB的直角頂點,已知AB=2OA,且點B的縱坐標大于0
(1)求 ![]() 的坐標;
的坐標;
(2)求圓C1:x2﹣6x+y2+2y=0關于直線OB對稱的圓C2的方程;在直線OB上是否存在點P,過點P的任意一條直線如果和圓C1圓C2都相交,則該直線被兩圓截得的線段長相等,如果存在求出點P的坐標,如果不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com