
【題目】已知數列{an}滿足(an+1﹣1)(an﹣1)=3(an﹣an+1),a1=2,令 ![]() .
.
(Ⅰ)證明:數列{bn}是等差數列;
(Ⅱ)求數列{an}的通項公式.
科目:高中數學 來源: 題型:
【題目】【選做題】
A.[選修4-1:幾何證明選講]
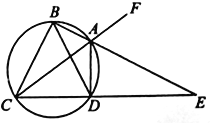
如圖,四邊形![]() 是圓的內接四邊形,
是圓的內接四邊形, ![]() ,
, ![]() 的延長線交
的延長線交![]() 的延長線于點
的延長線于點![]() .
.
求證: ![]() 平分
平分![]() .
.
B.[選修4-2:矩陣與變換]
已知變換![]() :
: ![]() ,試寫出變換
,試寫出變換![]() 對應的矩陣
對應的矩陣![]() ,并求出其逆矩陣
,并求出其逆矩陣![]() .
.
C.[選修4-4:坐標系與參數方程]
在平面直角坐標系![]() 中,已知直線
中,已知直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),曲線
為參數),曲線![]() 的參數方程為
的參數方程為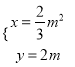 (
(![]() 為參數).若直線
為參數).若直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,求線段
兩點,求線段![]() 的長.
的長.
D.[選修4-5:不等式選講]
設![]() 均為正數,且
均為正數,且![]() ,求證
,求證 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}的前n項和為Sn , 且2Sn=(n+2)an﹣1(n∈N*).
(1)求a1的值,并用an﹣1表示an;
(2)求數列{an}的通項公式;
(3)設Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ,求證:Tn<
,求證:Tn< ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com