
【題目】已知函數![]() .
.
(1)若![]() ,求
,求![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)若![]() 在區間
在區間![]() 上恰有兩個零點,求
上恰有兩個零點,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)求出![]() ,利用導數的幾何意義求切線斜率為
,利用導數的幾何意義求切線斜率為![]() ,根據點斜式可得切線方程;(2)利用導數求出函數的極大值和極小值,利用
,根據點斜式可得切線方程;(2)利用導數求出函數的極大值和極小值,利用![]() 在區間
在區間![]() 上恰有兩個零點列不等式組,求解不等式組即可求
上恰有兩個零點列不等式組,求解不等式組即可求![]() 的取值范圍.
的取值范圍.
試題解析:(1)由已知得![]() ,
,
若![]() 時,有
時,有![]() ,
, ![]() ,
,
∴在![]() 處的切線方程為:
處的切線方程為: ![]() ,化簡得
,化簡得![]() .
.
(2)由(1)知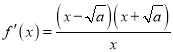 ,
,
因為![]() 且
且![]() ,令
,令![]() ,得
,得![]()
所以當![]() 時,有
時,有![]() ,則
,則![]() 是函數
是函數![]() 的單調遞減區間;、
的單調遞減區間;、
當![]() 時,有
時,有![]() ,則
,則![]() 是函數
是函數![]() 的單調遞增區間. 9分
的單調遞增區間. 9分
若![]() 在區間
在區間![]() 上恰有兩個零點,只需
上恰有兩個零點,只需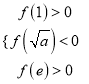 ,即
,即 ,
,
所以當![]() 時,
時, ![]() 在區間
在區間![]() 上恰有兩個零點.
上恰有兩個零點.
【方法點晴】本題主要考查利用導數求曲線切線以及利用導數研究函數零點問題,屬于難題.求曲線切線方程的一般步驟是:(1)求出![]() 在
在![]() 處的導數,即
處的導數,即![]() 在點
在點![]()
![]() 出的切線斜率(當曲線
出的切線斜率(當曲線![]() 在
在![]() 處的切線與
處的切線與![]() 軸平行時,在 處導數不存在,切線方程為
軸平行時,在 處導數不存在,切線方程為![]() );(2)由點斜式求得切線方程
);(2)由點斜式求得切線方程![]() .
.


科目:高中數學 來源: 題型:
【題目】某校高三期中考試后,數學教師對本次全部數學成績按![]() 進行分層抽樣,隨機抽取了20名學生的成績為樣本,成績用莖葉圖記錄如圖所示,但部分數據不小心丟失,同時得到如下表所示的頻率分布表:
進行分層抽樣,隨機抽取了20名學生的成績為樣本,成績用莖葉圖記錄如圖所示,但部分數據不小心丟失,同時得到如下表所示的頻率分布表:

(Ⅰ)求表中![]() ,
,![]() ,
,![]() 的值,并估計這次考試全校高三數學成績的及格率(成績在
的值,并估計這次考試全校高三數學成績的及格率(成績在![]() 內為及格);
內為及格);
(Ⅱ)設莖葉圖中成績在![]() 范圍內的樣本的中位數為
范圍內的樣本的中位數為![]() ,若從成績在
,若從成績在![]() 范圍內的樣品中每次隨機抽取1個,每次取出不放回,連續取兩次,求取出兩個樣本中恰好一個是數字
范圍內的樣品中每次隨機抽取1個,每次取出不放回,連續取兩次,求取出兩個樣本中恰好一個是數字![]() 的概率.
的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位生產A、B兩種產品,需要資金和場地,生產每噸A種產品和生產每噸B種產品所需資金和場地的數據如表所示:
資源 | 資金(萬元) | 場地(平方米) |
A | 2 | 100 |
B | 35 | 50 |
現有資金12萬元,場地400平方米,生產每噸A種產品可獲利潤3萬元;生產每噸B種產品可獲利潤2萬元,分別用x,y表示計劃生產A、B兩種產品的噸數.
(1)用x,y列出滿足生產條件的數學關系式,并畫出相應的平面區域;
(2)問A、B兩種產品應各生產多少噸,才能產生最大的利潤?并求出此最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=![]() ,an+1=3an-1(n∈N*).
,an+1=3an-1(n∈N*).
(1)若數列{bn}滿足bn=an-![]() ,求證:{bn}是等比數列;
,求證:{bn}是等比數列;
(2)求數列{an}的前n項和Sn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在銳角△ABC中,a,b,c分別是三個內角A,B,C的對邊,若2asinB= ![]() b. (Ⅰ)求A;
b. (Ⅰ)求A;
(Ⅱ)若a= ![]() ,△ABC的面積為
,△ABC的面積為 ![]() ,求△ABC的周長.
,求△ABC的周長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足(an+1﹣1)(an﹣1)=3(an﹣an+1),a1=2,令 ![]() .
.
(Ⅰ)證明:數列{bn}是等差數列;
(Ⅱ)求數列{an}的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() 對任意實數
對任意實數![]() ,都有
,都有![]() 恒成立.
恒成立.
(Ⅰ)證明: ![]() ;
;
(Ⅱ)若![]() ,求
,求![]() 的表達式;
的表達式;
(Ⅲ)在題(Ⅱ)的條件下設![]() ,若
,若![]() 圖象上的點都位于直線
圖象上的點都位于直線![]() 的上方,求實數
的上方,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A,B,C對應的邊分別為a,b,c(a≤b≤c),且bcosC+ccosB=2asinA. (Ⅰ)求角A;
(Ⅱ)求證: ![]() ;
;
(Ⅲ)若a=b,且BC邊上的中線AM長為 ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com