
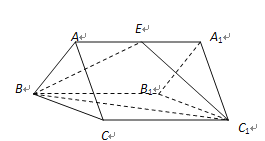
【題目】如圖:三棱柱![]() 的所有棱長均相等,
的所有棱長均相等,![]() ,
,![]() 為
為![]() 的中點.
的中點.
(1)求證:平面![]() ⊥平面
⊥平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)見解析;(2) ![]() .
.
【解析】試題分析:(1)連接CB1交BC1于點O,利用等腰三角形的三線合一證明線線垂直,再利用線面垂直的判定定理和面面垂直的判定定理進行證明;(2)取A1B1的中點
為H,連接C1H、BH,利用面面垂直的判定定理和性質定理得到線面垂直,即作出線面角,再利用直角三角形進行求解.
試題解析:(1)
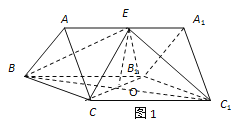
如圖1,連接CB1交BC1于點O,則O為CB1與BC1的中點,連接EC,EB1 依題意有EB=EC1=EC=EB1
∴EO⊥CB1,EO⊥BC1, ∴EO⊥平面BCC1B1,![]()
∴平面EBC1⊥平面BCC1B1,
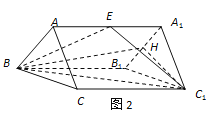
(2)如圖2取A1B1的中點為H,連接C1H、BH,
∵![]() ,∴平面A1B1C1⊥平面BB1A1A,
,∴平面A1B1C1⊥平面BB1A1A,
平面A1B1C1![]() 平面BB1A1A= A1B1,
平面BB1A1A= A1B1,
又∵A1C1=B1C1,H為A1B1的中點,∴C1H⊥A1B1,∴C1H⊥平面BB1A1A,
則∠C1BH為直線BC1與平面BB1A1A所成的角。
令棱長為2a,則C1H=![]() ,BC1=
,BC1=![]() ,
,
∴![]()
所以直線BC1與平面BB1A1A所成角的正弦值為![]()


 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源: 題型:
【題目】表示一位騎自行車和一位騎摩托車的旅行者在相距80 km的甲、乙兩城間從甲城到乙城所行駛的路程與時間之間的函數關系,有人根據函數圖象,提出了關于這兩個旅行者的如下信息:

①騎自行車者比騎摩托車者早出發3 h,晚到1 h;
②騎自行車者是變速運動,騎摩托車者是勻速運動;
③騎摩托車者在出發1.5 h后追上了騎自行車者;
④騎摩托車者在出發1.5 h后與騎自行車者速度一樣.
其中,正確信息的序號是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班主任對全班50名學生的學習積極性和對待班級工作的態度進行了調查,統計數據如下表所示:
積極參加班級工作 | 不太主動參加班級工作 | 合計 | |
學習積極性一般 | 6 | 19 | 25 |
合計 | 24 | 26 | 50 |
(1)如果隨機抽查這個班的一名學生,那么抽到積極參加班級工作的學生的概率是多少?抽到不太主動參加班級工作且學習積極性一般的學生的概率是多少?
(2)判斷是否有![]() 的把握認為學生的學習積極性與對待班級工作的態度有關系?
的把握認為學生的學習積極性與對待班級工作的態度有關系?
附:  , n=a+b+c+d.
, n=a+b+c+d.
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分14分)
如圖,四邊形![]() 是正方形,△
是正方形,△![]() 與△
與△![]() 均是以
均是以![]() 為直角頂點的等腰直角三角形,點
為直角頂點的等腰直角三角形,點![]() 是
是![]() 的中點,點
的中點,點![]() 是邊
是邊![]() 上的任意一點.
上的任意一點.
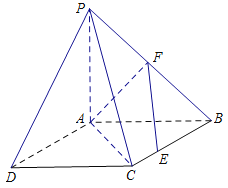
(1)求證: ![]() ;
;
(2)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某車間為了規定工時定額,需要確定加工零件所花費的時間,為此做了四次試驗,得到的數據如下表所示:
零件的個數x/個 | 2 | 3 | 4 | 5 |
加工的時間y/h | 2.5 | 3 | 4 | 4.5 |
(1)在給定的坐標系中畫出表中數據的散點圖;
(2)求出y關于x的線性回歸方程![]() ,并在坐標系中畫出回歸直線;
,并在坐標系中畫出回歸直線;
(3)試預測加工10個零件需要多少時間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】.如圖,在三棱錐V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD,則下列結論中不一定成立的是 ( )
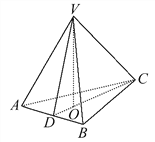
A. AC=BC
B. VC⊥VD
C. AB⊥VC
D. S△VCD·AB=S△ABC·VO
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com