
【題目】已知函數![]() .
.
(1)若![]() ,求函數
,求函數![]() 的圖像在點
的圖像在點![]() 處的切線方程;
處的切線方程;
(2)當![]() 時,函數
時,函數![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() 滿足以下兩個條件:①不等式
滿足以下兩個條件:①不等式![]() 的解集是
的解集是![]() ②函數
②函數![]() 在
在![]() 上的最小值是3.
上的最小值是3.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)若點![]() 在函數
在函數![]() 的圖象上,且
的圖象上,且![]() .
.
(ⅰ)求證:數列![]() 為等比數列
為等比數列
(ⅱ)令![]() ,是否存在正實數
,是否存在正實數![]() ,使不等式
,使不等式![]() 對于一切的
對于一切的![]() 恒成立?若存在,指出
恒成立?若存在,指出![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地建一座橋,兩端的橋墩已建好,這兩墩相距m米,余下工程只需建兩端橋墩之間的橋面和橋墩.經測算,一個橋墩的工程費用為256萬元;距離為x米的相鄰兩墩之間的橋面工程費用為(2+![]() )x萬元.假設橋墩等距離分布,所有橋墩都視為點,且不考慮其他因素,記余下工程的費用為y萬元.
)x萬元.假設橋墩等距離分布,所有橋墩都視為點,且不考慮其他因素,記余下工程的費用為y萬元.
(1)試寫出y關于x的函數關系式;
(2)當m=640米時,需新建多少個橋墩才能使y最小?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業有甲、乙兩條生產線生產同種產品,現隨機從這兩條生產線上各抽取20件產品檢測質量(單位:克),質量值落在![]() ,
, ![]() 的產品為三等品,質量值落在
的產品為三等品,質量值落在![]() ,
, ![]() 的產品為二等品,質量值落在
的產品為二等品,質量值落在![]() 的產品為一等品.下表為從兩條生產線上各抽取的20件產品的質量檢測情況,將頻率視為概率,從甲生產線上隨機抽取1件產品,為二等品的概率為0.2.
的產品為一等品.下表為從兩條生產線上各抽取的20件產品的質量檢測情況,將頻率視為概率,從甲生產線上隨機抽取1件產品,為二等品的概率為0.2.
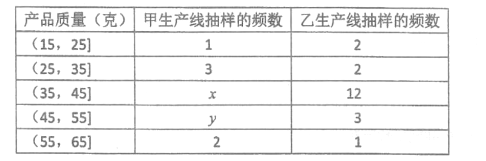
(1)求![]() 的值;
的值;
(2)現從兩條生產線上的三等品中各抽取1件,求這兩件產品的質量均在![]() 的概率;
的概率;
(3)估算甲生產線20個數據的中位數(保留3位有效數字).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 為梯形,
為梯形,![]() ,
,![]() ,且
,且![]() .
.

(Ⅰ)若點![]() 為
為![]() 上一點且
上一點且![]() ,證明:
,證明:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)在線段![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,說明理由.
的長;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點![]() ,
,![]() ,
,![]() 為坐標原點,點
為坐標原點,點![]() 滿足
滿足![]() =
=![]() +
+![]() ,(
,(![]() 為實數);
為實數);
(1)當點![]() 在
在![]() 軸上時,求實數
軸上時,求實數![]() 的值;
的值;
(2)四邊形![]() 能否是平行四邊形?若是,求實數
能否是平行四邊形?若是,求實數![]() 的值;若不是,請說明理由.
的值;若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com