
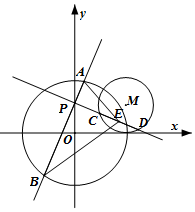
 在平面直角坐標系xOy中,過點P(0,1)且互相垂直的兩條直線分別與
在平面直角坐標系xOy中,過點P(0,1)且互相垂直的兩條直線分別與分析 (1)設直線AB的方程為:y=kx+1(k≠0),根據$AB=\frac{3}{2}\sqrt{7}$,利用弦長公式可得:$(\frac{3\sqrt{7}}{4})^{2}$+$(\frac{1}{\sqrt{1+{k}^{2}}})^{2}$=22,解得k,可得直線CD的方程,再利用弦長公式即可得出.
(2)①直線AB為y軸時,直線AB的方程為:x=0,直線CD的方程為:y=1.可得S△ABE=$\frac{1}{2}×|AB|•{x}_{E}$=4.
②直線AB的斜率存在時,設直線AB的方程為:y=kx+1,若k=0,則方程為y=1,經過圓心(2,1),此時△ABE不存在,舍去.k≠0時,可得直線CD的方程為:y=-$\frac{1}{k}$x+1.利用弦長公式可得:|AB|=2$\sqrt{\frac{3+4{k}^{2}}{1+{k}^{2}}}$.聯立$\left\{\begin{array}{l}{y=-\frac{1}{k}x+1}\\{(x-2)^{2}+(y-1)^{2}=1}\end{array}\right.$,化為:(k2+1)x2-4k2x+3k2=0,利用根與系數的關系、中點坐標公式可得E$(\frac{2{k}^{2}}{1+{k}^{2}},\frac{(k-1)^{2}}{1+{k}^{2}})$.利用點到直線的距離公式可得點E到直線AB的距離d.可得S△ABE=$\frac{1}{2}$|AB|•d=2$\sqrt{4-\frac{5{k}^{2}+4}{{k}^{4}+2{k}^{2}+1}}$,通過換元利用二次函數的單調性即可得出.
解答 解:(1)設直線AB的方程為:y=kx+1(k≠0),
∵$AB=\frac{3}{2}\sqrt{7}$,∴$(\frac{3\sqrt{7}}{4})^{2}$+$(\frac{1}{\sqrt{1+{k}^{2}}})^{2}$=22,
化為:k2=15,
解得k=$±\sqrt{15}$.
∴直線CD的方程為:y=$±\frac{1}{\sqrt{15}}$x+1.
∴|CD|=2$\sqrt{{1}^{2}-(\frac{±\frac{2}{\sqrt{15}}-1+1}{\sqrt{1+\frac{1}{15}}})^{2}}$=$\sqrt{3}$.
(2)①直線AB為y軸時,直線AB的方程為:x=0,直線CD的方程為:y=1.
S△ABE=$\frac{1}{2}×|AB|•{x}_{E}$=$\frac{1}{2}×4×2$=4.
②直線AB的斜率存在時,設直線AB的方程為:y=kx+1,
若k=0,則方程為y=1,經過圓心(2,1),此時△ABE不存在,舍去.
k≠0時,可得直線CD的方程為:y=-$\frac{1}{k}$x+1.
|AB|=2$\sqrt{{2}^{2}-(\frac{1}{\sqrt{1+{k}^{2}}})^{2}}$=2$\sqrt{\frac{3+4{k}^{2}}{1+{k}^{2}}}$.
聯立$\left\{\begin{array}{l}{y=-\frac{1}{k}x+1}\\{(x-2)^{2}+(y-1)^{2}=1}\end{array}\right.$,化為:(k2+1)x2-4k2x+3k2=0,
△=16k4-12(k2+1)k2>0,化為:k2>3.
∴x1+x2=$\frac{4{k}^{2}}{1+{k}^{2}}$,可得E$(\frac{2{k}^{2}}{1+{k}^{2}},\frac{(k-1)^{2}}{1+{k}^{2}})$.
∴點E到直線AB的距離d=$\frac{|\frac{2{k}^{3}}{1+{k}^{2}}-\frac{(k-1)^{2}}{1+{k}^{2}}+1|}{\sqrt{1+{k}^{2}}}$=$\frac{2|k|}{\sqrt{1+{k}^{2}}}$.
∴S△ABE=$\frac{1}{2}$|AB|•d=$\frac{1}{2}$×2$\sqrt{\frac{3+4{k}^{2}}{1+{k}^{2}}}$×$\frac{2|k|}{\sqrt{1+{k}^{2}}}$=2$\sqrt{\frac{{k}^{2}(3+4{k}^{2})}{(1+{k}^{2})^{2}}}$=2$\sqrt{4-\frac{5{k}^{2}+4}{{k}^{4}+2{k}^{2}+1}}$,
令k2+1=t>1,可得f(t)=$\sqrt{4-\frac{5t-1}{{t}^{2}}}$=$\sqrt{(\frac{1}{t}-\frac{5}{2})^{2}-\frac{9}{4}}$∈(0,2).
∴S△ABE∈(0,4).
綜上可得:S△ABE∈(0,4].
點評 本題考查了直線與圓相交弦長問題、弦長公式、點到直線的距離公式、三角形面積計算公式、二次函數的單調性、分類討論方法、相互垂直的直線斜率之間的關系,考查了推理能力與計算能力,屬于難題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
| A. | 54000 | B. | 100400 | C. | 100600 | D. | 100800 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
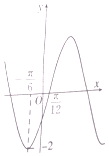
| A. | $(kπ-\frac{π}{6},kπ+\frac{π}{3}),k∈Z$ | B. | $(2kπ-\frac{π}{6},2kπ+\frac{π}{3}),k∈Z$ | ||
| C. | $(2kπ+\frac{π}{3},2kπ+\frac{5π}{6}),k∈Z$ | D. | $(kπ+\frac{π}{3},kπ+\frac{5π}{6}),k∈Z$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{π-2}{4π}$ | C. | $\frac{1}{2π}$ | D. | $\frac{3π+2}{4π}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
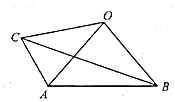 如圖,在四邊形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,則λ+μ的值為( )
如圖,在四邊形ABOC中,AO=BO=CO,AB=2,AC=1,∠BAC=120°,若$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,則λ+μ的值為( )| A. | $\frac{13}{6}$ | B. | $\frac{8}{3}$ | C. | $\frac{17}{6}$ | D. | $\frac{13}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-1,+∞) | B. | $[\frac{1}{8},+∞)$ | C. | $[-1,\frac{1}{8}]$ | D. | $[\frac{1}{8},1]$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{3}{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com