
【題目】已知數列![]() 滿足:
滿足:![]() ,
,![]() .
.
(1)求最小的正實數![]() ,使得對任意的
,使得對任意的![]() ,恒有
,恒有![]() ;
;
(2)求證:對任意的正整數![]() ,恒有
,恒有![]() .
.
【答案】(1)1;(2)證明見解析.
【解析】
試題分析:(1)已知條件是數列的遞推式,比較復雜,在證明時,可先計算數列的前幾項,如![]() .想象即歸納出結論數列
.想象即歸納出結論數列![]() 是遞減數列,從而
是遞減數列,從而![]() 的最小值為1,因此只要證明
的最小值為1,因此只要證明![]() ,可用數學歸納法證(2)
,可用數學歸納法證(2)
證明;(2)由(1)可得數列![]() 是單調遞減的正項數列.,這樣右邊的證明較方便,只要重新放縮可得,
是單調遞減的正項數列.,這樣右邊的證明較方便,只要重新放縮可得,
![]() ,從而
,從而![]() ,左邊不等式的證明較難,左邊先放縮為
,左邊不等式的證明較難,左邊先放縮為![]() ,從而
,從而![]() ,左右同除
,左右同除![]() 得:
得:![]() ,即
,即![]() ,利用累加法求
,利用累加法求![]() (其中求和
(其中求和![]() ,可用裂項相消或錯位相減法求得),可證明不等式.
,可用裂項相消或錯位相減法求得),可證明不等式.
試題解析:(1)由于![]() ,
,![]() ,
,![]() ,
,
由此我們可以猜想![]() 為單調遞減數列,因此我們猜測
為單調遞減數列,因此我們猜測![]() 的最小值為1,下面我們證明
的最小值為1,下面我們證明![]() .
.
![]() ,故當
,故當![]() 時,數列
時,數列![]() 為單調遞減數列,從而
為單調遞減數列,從而![]() .
.
![]() ,由于
,由于![]() ,且當
,且當![]() 時,有
時,有![]()
從而對任意的![]() ,恒有
,恒有![]() ,又由于
,又由于![]() ,從而所求的最小正實數
,從而所求的最小正實數![]() .
.
(說明:若用數學歸納法證明,也同樣給滿分)
事實上,由于![]() ,假設
,假設![]() 時,
時,![]() ,則當
,則當![]() 時,
時,
考慮到![]() ,從而
,從而![]() ,
,![]() .
.
從而![]() ,
,
從而由數學歸納法原理得:對任意的![]() ,恒有
,恒有![]() .
.
又由于![]() ,從而所求的最小正實數
,從而所求的最小正實數![]() .
.
(2)由于![]() ,則
,則![]() ,
,
從而數列![]() 是單調遞減的正項數列.
是單調遞減的正項數列.
一方面,![]() ,從而
,從而![]()
另一方面,![]() ,從而
,從而![]() ,
,
左右同除![]() 得:
得:![]() ,即
,即![]()
設
![]() (也可利用錯位相減法求解
(也可利用錯位相減法求解 ,兩式相減得
,兩式相減得
![]() ,從而
,從而
![]() )
)
從而由![]() ,得,
,得,
當![]() 時,
時,![]()
從而![]() ,即
,即 ,
,
即當![]() 時,
時,![]() ,又當
,又當![]() 時,
時,![]() ,從而對任意的
,從而對任意的![]() ,恒有
,恒有![]() .
.
綜上所示,對任意的正整數![]() ,恒有
,恒有![]() .
.


 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,圓![]() 的方程為
的方程為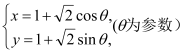 .以坐標原點
.以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,建立極坐標系,兩種坐標系中取相同的單位長度,直線
軸的正半軸為極軸,建立極坐標系,兩種坐標系中取相同的單位長度,直線![]() 的極坐標方程
的極坐標方程![]() .
.
(Ⅰ)當![]() 時,判斷直線
時,判斷直線![]() 與
與![]() 的關系;
的關系;
(Ⅱ)當![]() 上有且只有一點到直線
上有且只有一點到直線![]() 的距離等于
的距離等于![]() 時,求
時,求![]() 上到直線
上到直線![]() 距離為
距離為![]() 的點的坐標.
的點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大衍數列,來源于《乾坤譜》中對易傳“大衍之數五十”的推論.主要用于解釋中國傳統文化中的太極衍生原理.數列中的每一項,都代表太極衍生過程中,曾經經歷過的兩儀數量總和,是中華傳統文化中隱藏著的世界數學史上第一道數列題.其前10項依次是0,2,4,8,12,18,24,32,40,50,…則此數列第20項為
A. 180 B. 200 C. 128 D. 162
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系中,以原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() ,過點
,過點![]() 的直線
的直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),
為參數),![]() 與
與![]() 分別交于
分別交于![]() .
.
(Ⅰ)寫出![]() 的平面直角坐標系方程和
的平面直角坐標系方程和![]() 的普通方程;
的普通方程;
(Ⅱ)若![]() 成等比數列,求
成等比數列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從一箱產品中隨機地抽取一件,設事件A={抽到一等品},事件B={抽到二等品},事件C={抽到三等品},且已知P(A)=0.65,P(B)=0.2,P(C)=0.1.則事件“抽到的是二等品或三等品”的概率為( )
A. 0.7 B. 0.65
C. 0.35 D. 0.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】要從容量為102的總體中用系統抽樣法隨機抽取一個容量為9的樣本,則下列敘述正確的是( )
A. 將總體分11組,每組間隔為9
B. 將總體分9組,每組間隔為11
C. 從總體中剔除3個個體后分11組,每組間隔為9
D. 從總體中剔除3個個體后分9組,每組間隔為11
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】利用斜二測畫法畫水平放置的平面圖形的直觀圖,得到下列結論,其中正確的是( )
A.正三角形的直觀圖仍然是正三角形
B.平行四邊形的直觀圖一定是平行四邊形
C.正方形的直觀圖是正方形
D.圓的直觀圖是圓
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用樣本估計總體,下列說法正確的是( )
A、樣本的結果就是總體的結果
B、樣本容量越大,估計就越精確
C、樣本的標準差可以近似地反映總體的平均狀態
D、數據的方差越大,說明數據越穩定
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com