
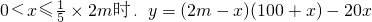 (2分)
(2分)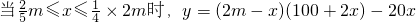 (4分)
(4分)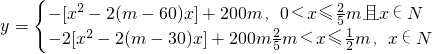 ,
,
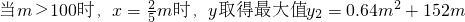 (8分)
(8分)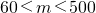 ,∴
,∴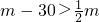 ,
,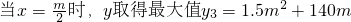
 ,
, 時,獲得的經(jīng)濟效益最大. (16分)
時,獲得的經(jīng)濟效益最大. (16分)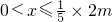 和
和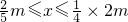 兩種情況下函數(shù)的解析式,列出分段函數(shù);分別對分段函數(shù)進行參數(shù)的討論,最后得出裁員的最佳人數(shù).
兩種情況下函數(shù)的解析式,列出分段函數(shù);分別對分段函數(shù)進行參數(shù)的討論,最后得出裁員的最佳人數(shù).

 口算能手系列答案
口算能手系列答案科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(09年江蘇百校樣本分析)(15分)某公司為了應(yīng)對金融危機,決定適當(dāng)進行裁員.已知這家公司現(xiàn)有職工![]() 人(
人(![]() ,且
,且![]() 為10的整數(shù)倍),每人每年可創(chuàng)利100千元. 據(jù)測算,在經(jīng)營條件不變的前提下,若裁員人數(shù)不超過現(xiàn)有人數(shù)的20%,則每裁員1人,留崗員工每人每年就能多創(chuàng)利1千元;若裁員人數(shù)超過現(xiàn)有人數(shù)的20%,則每裁員1人,留崗員工每人每年就能多創(chuàng)利2千元. 為保證公司的正常運轉(zhuǎn),留崗的員工數(shù)不得少于現(xiàn)有員工人數(shù)的75%. 為保障被裁員工的生活,公司要付給被裁員工每人每年20千元的生活費. 問:為了獲得最大的經(jīng)濟效益,該公司應(yīng)裁員多少人?
為10的整數(shù)倍),每人每年可創(chuàng)利100千元. 據(jù)測算,在經(jīng)營條件不變的前提下,若裁員人數(shù)不超過現(xiàn)有人數(shù)的20%,則每裁員1人,留崗員工每人每年就能多創(chuàng)利1千元;若裁員人數(shù)超過現(xiàn)有人數(shù)的20%,則每裁員1人,留崗員工每人每年就能多創(chuàng)利2千元. 為保證公司的正常運轉(zhuǎn),留崗的員工數(shù)不得少于現(xiàn)有員工人數(shù)的75%. 為保障被裁員工的生活,公司要付給被裁員工每人每年20千元的生活費. 問:為了獲得最大的經(jīng)濟效益,該公司應(yīng)裁員多少人?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年江蘇省鹽城中學(xué)高三(下)開學(xué)數(shù)學(xué)試卷(解析版) 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011年江蘇省無錫市江陰市成化高中高考數(shù)學(xué)模擬試卷2(理科)(解析版) 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:同步題 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com