【答案】
分析:(1)設分成的兩段分別為x、y,則第三段為10-x-y,得到所有情況下的不等式組和能構成三角形的不等式組,在坐標系內作出兩個不等式組對應的平面區域,分別計算它們的面積,用幾何概型計算公式即可得到三段能構成三角形的概率.
(2)用列舉的方法,找出三段均為正整數的所有情況總數,再從中找出能構成三角形的情況數,用古典概型計算公式即可算出三段能構成三角形的概率.
解答:解:(1)設分成的兩段分別為x、y,則第三段為10-x-y,則有
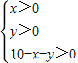
,…(1)
如果能構成三角形,則有
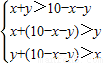
,即
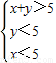
(2)
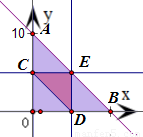
在坐標系內作出兩個不等式組對應的平面區域,得到如圖所示
不等式(1)對應的區域為△OAB及其內部,其中A(0,10),B(10,0),O為坐標原點
不等式(2)對應的區域為△CDE及其內部,其中C(0,5),D(5,0),E(5,5)
∵S
△OAB=

×10×10=50,S
△CDE=

×5×5=
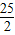
,
∴分成的三段能構成三角形的概率為P
1=
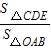
=

(2)將該線段分成三段均為正整數,只要確定其中兩邊長度即可得到三邊長度
∵其中兩段的情況共有(1,1),(1,2),(1,3),(1,4),
(1,5),(1,6),(1,7),(1,8),(2,1),(2,2),…(8,1)共36種,
能構成三角形的情況有(2,4),(3,3),(3,4),(4,2),(4,3),(4,4)共6種,
∴分成的三段長度恰好都為整數且這三段能構成三角形的概率為P
2=
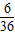
=

答:(1)分成的三段能構成三角形的概率為

;(2)分成的三段長度恰好都為整數且這三段能構成三角形的概率為

.
點評:本題給出長度為10的線段分成3段,求這三段能構成三角形的概率,著重考查了幾何概型、古典概型等計算公式知識,屬于中檔題.

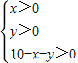 ,…(1)
,…(1)
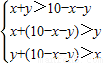 ,即
,即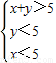 (2)
(2) ×10×10=50,S△CDE=
×10×10=50,S△CDE= ×5×5=
×5×5=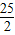 ,
,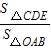 =
=
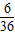 =
=
 ;(2)分成的三段長度恰好都為整數且這三段能構成三角形的概率為
;(2)分成的三段長度恰好都為整數且這三段能構成三角形的概率為 .
.
